A Brief History of Time Measurement

Ever since humans first noticed the regular movement of the Sun and the stars, we have wondered about the passage of time. Prehistoric people first recorded the phases of the Moon some 30,000 years ago, and recording time has been a way by which humanity has observed the heavens and represented the progress of civilization.

 

Natural Events

The earliest natural events to be recognised were in the heavens, but during the course of the year there were many other events that indicated significant changes in the environment. Seasonal winds and rains, the flooding of rivers, the flowering of trees and plants, and the breeding cycles or migration of animals and birds, all led to natural divisions of the year, and further observation and local customs led to the recognition of the seasons.

 

 

Measuring time by the Sun, the Moon and the Stars

 

As the sun moves across the sky, shadows change in direction and length, so a simple sundial can measure the length of a day. It was quickly noticed that the length of the day varies at different times of the year. The reasons for this difference were not discovered until after astronomers accepted the fact that the earth travels round the sun in an elliptic orbit, and that the earth's axis is tilted at about 26 degrees. This variation from a circular orbit leads to the Equation of Time (see 'Note 2' below) which allows us to work out the difference between 'clock' time and 'sundial time'.

 

Another discovery was that sundials had to be specially made for different latitudes because the Sun's altitude in the sky decreases at higher latitudes, producing longer shadows than at lower latitudes. Today, artists and astronomers find many ways of creating modern sundials.

 

 

A sundial with roman numerals. As you look at this dial, which direction are you facing?

The progress of the sun can be recorded using the four faces of this cube. Can you discover the orientation of these faces?

Wall Sundial

 

 

Prehistoric carving said to represent the Orion constellation

The oldest image of a star pattern, the constellation of Orion, has been recognised on a piece of mammoth tusk some 32,500 years old. The constellation Orion is symbolized by a man standing with his right arm raised and a sword at his belt and can be seen throughout the world at different times of the year. Orion was the sun god of the Egyptians and Phonecians and called the 'strong one' by the Arabs. In parts of Africa, his belt and sword are known as 'three dogs chasing three pigs' and the Borana people of East Africa based a sophisticated calendar on observations of star clusters near Orion's belt. Orion contains some of the brightest stars in the southern part of the winter sky in the northern hemisphere and can be seen later in the southern hemisphere.

The three stars of Orion's belt and the red star of his right arm can be easily recognised

The earliest Egyptian Star Map is about 3,500 years old and shows the most unusual conjunction of the planets (Venus, Mercury, Saturn and Jupiter) in the constellation of Orion and the occurrence of a solar eclipse that happened in 1534 BCE.

Babylonian records of observations of heavenly events date back to 1,600 BCE. The reason for adopting their arithmetic system is probably because 60 has many divisors, and their decision to adopt 360 days as the length of the year and 3600 in a circle was based on their existing mathematics and the convenience that the sun moves through the sky relative to fixed stars at about 1degree each day.   The constellation Taurus, the bull, a symbol of strength and fertility, figures prominently in the mythology of nearly all early civilizations, from Babylon and India to northern Europe. The Assyrian winged man-headed bull had the strength of a bull, the swiftness of a bird and human intelligence.

From about 700 BCE the Babylonians began to develop a mathematical theory of astronomy, but the equally divided 12-constellation zodiac appears later about 500 BCE to correspond to their year of 12 months of 30 days each. Their base 60 fraction system which we still use today (degrees / hours, minutes and seconds) was much easier to calculate with than the fractions used in Egypt or Greece, and remained the main calculation tool for astronomers until after the 16th century, when decimal notation began to take over.

The earliest archaeological evidence of Chinese calendars appears about 2,000 BCE. They show a 12 month year with the occasional occurrence of a 13th month. However, traditional Chinese records suggest the origin of a calendar of 366 days depending on the movements of the Sun and the Moon as early as 3,000 BCE. Over such a long period of observation, Chinese astronomers became aware that their calendar was not accurate, and by the second century CE it was recognised that the calendar became unreliable every 300 years. This problem is called Precession and was recorded by Chinese historians in the fourth and fifth centuries CE. In the fifth century CE the scholar Zu Chongzi created the first calendar which took precession into account, and the most comprehensive calendar was the Dayan Calendar compiled in the Tang Dynasty (616-907 CE) well ahead of any such development in Europe.

 

 

 

Precession is due to the gradual movement of the Earth's rotational axis in a circle with respect to the fixed stars. This movement produces a slow 'wobble' which means that the positions of the stars complete a cycle of about 26,000 years.   The Earth's axis completes a circuit about once every 26,000 years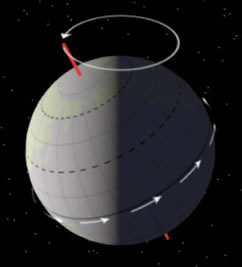

In the Mediterranean, Hipparchus made the earliest calculations of precession in about 160 BCE. The problem was taken up by astronomers in the Middle East and India who recognized that precession gradually altered the length of the year. Calendars have had to be altered regularly. In 325 CE the spring (vernal) equinox had moved to March 21. The Emperor Constantine established dates for the Christian holidays, but Easter is based on the date of the vernal equinox which varies every year because the equinox is an astronomical event. By 1582 the vernal equinox had moved another ten days and Pope Gregory established a new calendar, and this change is the reason for having an extra day in every leap year. However, there are still small changes accumulating, and one day we shall have to adopt a new calendar!

Inventions for measuring and regulating time

The early inventions were made to divide the day or the night into different periods in order to regulate work or ritual, so the lengths of the time periods varied greatly from place to place and from one culture to another.

 

 

 

Oil Lamps

There is archaeological evidence of oil lamps about 4,000 BCE, and the Chinese were using oil for heating and lighting by 2,000 BCE. Oil lamps are still significant in religious practices, symbolic of the journey from darkness and ignorance to light and knowledge. The shape of the lamp gradually evolved into the typical pottery style shown. It was possible to devise a way of measuring the level in the oil reservoir to measure the passing of time.

  Clay Oil lamp

Candle timer 

Candle Clocks

Marked candles were used for telling the time in China from the sixth century CE. There is a popular story that King Alfred the Great invented the candle clock, but we know they were in use in England from the tenth century CE. However, the rate of burning is subject to draughts, and the variable quality of the wax. Like oil lamps, candles were used to mark the passage of time from one event to another, rather than tell the time of day.

Water Clocks

The water clock, or clepsydra, appears to have been invented about 1,500 BCE and was a device which relied on the steady flow of water from or into a container. Measurements could be marked on the container or on a receptacle for the water. In comparison with the candle or the oil lamp, the clepsydra was more reliable, but the water flow still depended on the variation of pressure from the head of water in the container.

 

Astronomical and astrological clock making was developed in China from 200 to 1300 CE. Early Chinese clepsydras drove various mechanisms illustrating astronomical phenomena. The astronomer Su Sung and his associates built an elaborate clepsydra in 1088 CE. This device incorporated a water-driven bucket system originally invented about 725 CE. Among the displays were a bronze power-driven rotating celestial globe, and manikins that rang gongs, and indicated special times of the day.

Clepsydra

Improvements were made to regulate the flow by maintaining a constant head of water

Su Sung water clock

Su Sung's astronomical water clock

sand glass

Sandglass

Hour Glasses or Sandglasses

As the technology of glass-blowing developed, from some time in the 14th century it became possible to make sandglasses. Originally, sandglasses were used as a measure for periods of time like the lamps or candles, but as clocks became more accurate they were used to calibrate sandglasses to measure specific periods of time, and to determine the duration of sermons, university lectures, and even periods of torture.

The Division of the Day and the Length of the 'Hour'

An Egyptian sundial from about 1,500 BCE is the earliest evidence of the division of the day into equal parts, but the sundial was no use at night. The passage of time was extremely important for astronomers and priests who were responsible for determining the exact hour for the daily rituals and for the important religious festivals, so a water clock was invented.

Egyptian water clock

The Merkhet

The Egyptians improved upon the sundial with a 'merkhet', one of the oldest known astronomical instruments. It was developed around 600 BCE and uses a string with a weight as a plumb line to obtain a true vertical line, as in the picture. The other object is the rib of a palm leaf, stripped of its fronds and split at one end, making a thin slit for a sight.

 

A pair of merkhets were used to establish a North-South direction by lining them up one behind the other with the Pole Star. Viewing the plumb lines through the sight made sure the two merkhets and the sight were in the same straight line with the Pole Star. This allowed for the measurement of night-time events with a water clock when certain stars crossed the vertical plumb line (a 'transit line'), and these events could then be recorded by 'night-time lines' drawn on a sundial.

See also 'Note 1' below.

Egyptian Merkhet

 

An Egyptian Merkhet. The wooden upright has a notch to use as a sight when using two plumb lines

There are various theories about how the 24 hour day developed. The fact that the day was divided into 12 hours might be because 12 is a factor of 60, and both the Babylonian and Egyptian civilisations recognised a zodiac cycle of 12 constellations. On the other hand, (excuse the pun) finger-counting with base 12 was a possibility. The fingers each have 3 joints, and so counting on the joints gives one 'full hand' of 12.

.

In about 50 BCE Andronikos of Kyrrhestes, built the Tower of Winds in Athens. This was a water clock combined with Sundials positioned in the eight principal wind directions. By then it was the most accurate device built for keeping time.

Tower of Winds

The Tower of the Winds in Athens contained a clepsydra and shows the North-East, North and North-West deities in this picture

Hours did not have a fixed length until the Greeks decided they needed such a system for theoretical calculations. Hipparchus proposed dividing the day equally into 24 hours which came to be known as equinoctial hours. They are based on 12 hours of daylight and 12 hours of darkness on the days of the Equinoxes. However, ordinary people continued to use seasonally varying hours for a long time. Only with the advent of mechanical clocks in Europe in the 14th Century, did the system we use today become commonly accepted.

 

 

Earliest mechanical clock

Mechanical clocks replaced the old water clocks, and the first clock escapement mechanism appears to have been invented in 1275. The first drawing of an escapement was given by Jacopo di Dondi in 1364. In the early-to-mid-14th century, large mechanical clocks began to appear in the towers of several cities. There is no evidence or record of the working models of these public clocks that were weight-driven. All had the same basic problem: the period of oscillation of the mechanism depended heavily on the driving force of the weights and the friction in the drive.

In later Mediaeval times elaborate clocks were built in public places. This is the Astronomical clock in Prague, parts of which date from about 1410.

 

 

 

 

Weight clock Prague astronomical clock

This mechanism illustrates a basic escapement. The weight rotates the drum which drives the toothed wheel which gives the mechnism its "tick-tock" movement

Prague Astronomical Clock

Showing the Zodiac Circles and early versions of the digits 2, 3, 4 and 7

The earliest surviving spring driven clock can be found in the science museum in London and dates from about 1450. Replacing the heavy drive weights with a spring permitted smaller and portable clocks and watches.

More Accurate Mechanical Clocks

Christiaan Huygens made the first pendulum clock, regulated by a mechanism with a "natural" period of oscillation in 1656. Galileo studied pendulum motion as early as 1582, but his design for a clock was not built before his death. Huygens' pendulum clock had an error of less than 1 minute a day, and his later refinements reduced his clock's errors to less than 10 seconds a day.

There was no device for keeping accurate time at sea until John Harrison, a carpenter and instrument maker, refined techniques for temperature compensation and found new ways of reducing friction. By 1761, he had built a marine chronometer with a spring and balance wheel escapement that kept very accurate time. With the final version of his chronometer, which looked like a large pocket watch, he achieved a means of determining longitude to within one-half a degree.

It was not until 1884 that a conference at Greenwich reached agreement on global time measurement and adopted Greenwich Mean Time as the international standard. Today we rely on atomic clocks for our most accurate time measurements.

Pendulum clock

The pendulum moves the lever which creates the rocking movement of the escapement N.B. Pedagogical notes related to measurement and time can be found by clicking on the " Notes " tab at the top of this article.

Supporting notes

Note 1

When you think about the problem - we can find due South easily from the sun at midday. Looking at the night sky, we eventually deduce that there is a fixed point in the heavens around which all the stars rotate once every day (24 hours). This is where we find the 'Pole Star' (from the Great Bear or Ursa Major, measure the distance of about four lengths of the two stars at the end, 'the pointers' to find Polaris). This is the Celestial Pole - which was different for the Egyptians from today because of the phenomenon of Precession.

Up to about 1,900 BCE the Celestial Pole was Thuban a star in the 'tail' of the constellation Draco. By 1,000 BCE it was Thuban in the constellation Ursa Minor. Today Polaris is the last star in the 'tail' of Ursa Minor.

Note 2

'Sun time' and 'clock time' are different. Sun time is based on the fact that the sun reaches its highest point (the meridian), in the middle of the day, and on the next day at its highest point, it will have completed a full cycle. However, the time between the sun reaching successive meridians is often different from clock time. According to clock time, from May to August, the day is close to 24 hours, but in late October the days are about 15 minutes shorter, while in mid February the days are about 14 minutes longer. For our daily routines, it is important to have a constant 'clock time' of 24 hours. This variation is called the 'Equation of Time' and shows the relationship between sun time and clock time. The variation has two causes; the plane of the Earth's equator is inclined to the Earth's orbit around the Sun, and the orbit of the Earth around the sun is an ellipse and not a circle. The National Maritime Museum website shows two separate graphs for these causes, and a third graph where they are combined to give the full correction.

A Beautiful Proof: Why the Limit of sin(x)/x as x Approaches 0 is 1?

From the day I learned Calculus, I noticed that I had become obsessed with learning how certain things worked. While it is fun to understand how certain things work, it is even more entertaining to learn about how something was discovered. Furthermore, it is most amusing to learn how something works or exists on our own. For example, knowing that 2•2=4 isn’t very rewarding for a child. However, understanding why 2•2=4, demonstrating it with wooden blocks, is extremely rewarding.

That is why it is so enjoyable to come up with and read about proofs. To write out a proof takes skill outside of coming up with it. Many times, brilliant people struggle to write out why certain things are the way they are. Putting into writing a certain proof should have its own education. Sadly, schools don’t teach students about proofs, what they are, and how they are come up with. I genuinely hope this will get mended soon. If you want to learn how to fabricate proofs, I suggest you read ‘How to solve it’ by George Polya.

First of all, I would like to mention that the person who first proved the theorem I will demonstrate below didn’t stumble upon it accidentally. He discovered this truth because he is a brilliant individual. Furthermore, he performed this with a few fundamental trigonometric ideas. That shows that you can also find beautiful mathematical proofs and truths with a simple amount of knowledge.

We must remember that just because one person has proved a theorem doesn’t mean that you can’t verify it independently as well. If you can prove said theorem sitting at home, that theorem now belongs to you. It doesn’t matter whether the rest of the world acknowledges it as your theorem.

I saw a very famous theorem amongst AP Calculus students on Khan Academy. I will unravel its proof step-by-step below and it may seem complicated to some but is quite simple. Mathematicians like proofs to be simplified and clean. The fact that there are many writings and equations never shadows the beauty of the proof. This proof may be long-winded, but this is because I have tried to provide details about every piece of information. If you near the middle of the proof and don’t still understand it, please don’t panic. You need to read a little more carefully.

Claim: The limit of sin(x)/x as x approaches 0 is 1.

To build the proof, we will begin by making some trigonometric constructions. When you think about trigonometry, your mind naturally wanders to the unit circle. By definition, a unit circle is a circle with a radius of 1. To perform trigonometric operations on it, we first divide it into four equal portions.

Unit Circle: The unit circle is the circle of radius one centered at the origin (0, 0) in the

 Cartesian coordinate system in the Euclidean plane.

Proof: First, we will build our proof in the first quadrant of the unit circle. To start, let’s make two similar triangles, ABC and ADE. Color the smaller triangle, ABC, green to distinguish it. If you’ll notice, both the triangle’s hypotenuses are on the same line.

Definition: “Hypotenuse” is the longest side of a right triangle, opposite the right angle.

Per definition, the radius of the unit circle is equal to 1. Therefore, the hypotenuse, AC, of the smaller triangle must be 1. Then what is BC equal to? Point C will be at the intersection of the radius we drew and the unit circle, meaning that the length of BC is equal to the y value of point C.

If we wanted to find the sin value of x, by definition, it would have to be sin(x) = BC/1.

 Therefore, BC = sin(x). It is imperative to remember that while sin(x) is equal to a number 

since we don’t know the number yet, we define it as sin(x).

Note: Since sin(x) identifies a length, it must be positive. Therefore, we must show sin(x) as an absolute value, |sin(x)|. Furthermore, if we do this, we will get the same answer if we work in the other quadrants.

As you can see, we have defined the length of BC using a trigonometric function. If we can do this for the BC side of ABC, we can also use a trigonometric function to define the DE side of ADE.

Since we don’t know the hypotenuse of the triangle ADE, let’s use a different function to

define it. Since the length of AD in the triangle ADE is equal to the radius of the unit circle, 

it makes sense to use the tangent function. That is because tan(x) is equal to opposite over

 adjacent. Meaning, tan(x) = DE/1. And since we are working on the unit circle, we get DE = tan(x).

Note: The adjacent side is the non-hypotenuse side that is next to a given angle.

Again, since tan(x) represents a length here, it must always be positive. Therefore, we use absolute value, giving us |tan(x)|.

Excellent! We have almost found all of the side lengths. Now, what should we do?

Since we have found almost all side lengths, let’s deal with a little bit of area calculation. To do this, let’s connect the corners C and D with a line and call this new triangle within the circle, triangle ACD. Now we can color the empty space of this triangle blue.

Perfect. Now we can work on the triangle ACD, composed of yellow and blue. How can we represent the area triangle ACD? There is a neat fact that we know regarding triangles; the area of any triangle is half of the product of the base multiplied by the height.

The base length of ACD is equal to 1, as is very clear. The height is equal to BC, and as we

concluded earlier, BC is equal to |sin(x)|. Therefore, the area of triangle ACD is equal

 to 1•|sin(x)| / 2, or |sin(x)|/2. (Absolute value of sin of x over two)

We have found the area of triangle ACD. Next, we need to find the area of the ACD portion of our circle (green area + blue area + orange area).

We already know how to find the area of a circle. The area of a circle is π times radius square. However, we don’t need the entire area. We only want the green area + blue area + orange area. Therefore, we need to find the ratio of the desired area to the entire area. Here, we can use the following logic.

Note: If we were to go all the way around the circle, it would be 2π radians, right? Therefore, 

the portion that angle x covers to the entire circle is x/2π.

The logic mentioned above will be of utmost use to us as we work on the unit circle. Since the radius of the unit circle is 1, using the πr² formula, we know that the area is just pi. Since if we put one instead of r, 1²=1.

Truth: The area of a unit square is just π.

We can now find the area of the ACD portion of the circle. The area of the circle is

equal to π, and the ratio of the shaded area to the entire area is x/2π. Therefore, the 

area of ACD (green area + blue area + orange area) is equal to x/2π * π, or x/2. Furthermore, 

since the area has to be a positive value, we again use absolute value symbols.

Now we can brainstorm on the area of the largest triangle, triangle ADE. Actually, finding the area is relatively straightforward as all we have to do is divide the product of length AD and length DE by 2. Somewhere above, we found that the length of DE to be |tan(x)|. Since the length of AD is equal to the radius, it is equal to 1. Therefore, the area of triangle ADE is |tan(x)|/2. Perfect!

What will we do with these area values, though? We will compare them to each other. How though? We have the areas of triangles ABC, ACD, and ADE, and the ACD portion of the circle that we can compare. As we can see, the area of triangle ACD is less than or equal to the area of the ACD portion of the circle. Furthermore, the circle’s ACD portion is less than or equal to the area of triangle ADE. Therefore,

|sin(x)|/2 ≤ x/2 ≤|tan(x)|/2

So far, so good. Now, we have to manipulate this inequality a little bit. One thing we have to be wary of, however, is making sure to keep the inequality balanced. For example, instead of 3, we can write 6/2, and it will remain the same.

Since the terms in the inequality are divided by 2, we can multiply them by 2 to eliminate the denominator, simplifying the inequality. That gives us, the absolute value of sin of x is less than or equal to the absolute value of x, which is less than or equal to the absolute value of the tangent of x.

|sin(x)| ≤ x ≤|tan(x)|

At this point, we can manipulate the tangent function and write it differently. That is because the tangent of x is equal to the sin of x over the cosine of x.

|sin(x)| ≤ x ≤ |sin(x)|/|cos(x)|

As you can see, we have achieved a very different inequality. However, we need to manipulate the inequality further. We can now divide all of the terms by the absolute value of x. That will result in the following inequality.

|sin(x)|/|sin(x)| ≤ x/|sin(x)| ≤ |sin(x)|/|cos(x)|• 1/|sin(x)|

Note: Since we’re dividing by a positive quantity, it’s not going to change the direction of the inequalities.

We can now achieve 1 ≤ x/|sin(x)| ≤ 1/|cos(x)| by simplifying our latest inequality.

At this point, it is essential to remember our purpose. Remember, we want to prove the “sin of x over x.” If you look at the inequality, we realize that we have “x over the sin of x.” In this situation, there is one thing you have to remember. Yes, reciprocals.

Reciprocal: The multiplicative inverse. If you take the reciprocal of a fraction a/b, you get b/a.

If we take the reciprocal of everything, we get the “sin of x over x.” There is one thing we mustn’t forget, though, changing the direction of the inequality. Thus, the less than or equal to sign will turn into the greater than or equal to sign.

We are lucky because the reciprocal of 1 is still 1. Therefore, the new inequality is as follows.

1  ≥ |sin(x)|/x  ≥ |cos(x)|

Note: We only care about the first and fourth quadrants. In the first quadrant, the sin of “x” and “x” are both positive. In the fourth quadrant, they’re both negative, but you’re going to get a positive value when you divide them. So we can erase those absolute value signs. Also, since the cosine value is also positive, we can get rid of the absolute value signs.

1  ≥ sin(x)/x  ≥ cos(x)

Hang on, hang on. We are almost done. In the inequality, all of the terms represent functions.

Therefore, we can say that f(x) = 1, g(x) = sin(x)/x, and h(x) = cos(x). We say this 

because if we want to find the limits we have been looking for, we need to rely on 

some theorems.

Meaning that if in one inequality, the limits of both the left and the right functions 

are approaching the same value, the middle function’s limit also has to approach to the

 same value.1  ≥ sin(x)/x  ≥ cos(x)

Therefore, if we look at our inequality, it is clear that the first function, f(x), approaches 1. How about h(x)? Meaning, what is the limit as x approaches zero of cosine x? Yes, the cosine of zero is just one, and cosine is a continuous function. Therefore, the limit is 1.

So our limit is going to be less than or equal to one. It is also going to be greater than or equal to one. Therefore, it must be equal to one.

We are now done!

हमारे भारत के गौरव श्रीनिवास रामानुजन

श्रीनिवास रामानुजन्  (22 दिसम्बर 1887 – 26 अप्रैल 1920) एक महान भारतीय गणितज्ञ थे। इन्हें आधुनिक काल के महानतम गणित विचारकों में गिना जाता है। इन्हें गणित में कोई विशेष प्रशिक्षण नहीं मिला, फिर भी इन्होंने विश्लेषण एवं संख्या सिद्धांत के क्षेत्रों में गहन योगदान दिए। इन्होंने अपने प्रतिभा और लगन से न केवल गणित के क्षेत्र में अद्भुत अविष्कार किए वरन भारत को अतुलनीय गौरव भी प्रदान किया
ये बचपन से ही विलक्षण प्रतिभावान थे। इन्होंने खुद से गणित सीखा और अपने जीवनभर में गणित के 3,884 प्रमेयों का संकलन किया। इनमें से अधिकांश प्रमेय सही सिद्ध किये जा चुके हैं। इन्होंने गणित के सहज ज्ञान और बीजगणित प्रकलन की अद्वितीय प्रतिभा के बल पर बहुत से मौलिक और अपारम्परिक परिणाम निकाले जिनसे प्रेरित शोध आज तक हो रहा है, यद्यपि इनकी कुछ खोजों को गणित मुख्यधारा में अब तक नहीं अपनाया गया है। हाल में इनके सूत्रों को क्रिस्टल-विज्ञान में प्रयुक्त किया गया है। इनके कार्य से प्रभावित गणित के क्षेत्रों में हो रहे काम के लिये रामानुजन जर्नल की स्थापना की गई है।

आरंभिक जीवनकाल   

रामानुजन का जन्म 22 दिसम्बर1887 को भारत के दक्षिणी भूभाग में स्थित कोयंबटूर के ईरोड नामके गांव में हुआ था। वह पारंपरिक ब्राह्मण परिवार में जन्मे थे। इनकी की माता का नाम कोमलताम्मल और इनके पिता का नाम श्रीनिवास अय्यंगर था। इनका बचपन मुख्यतः कुंभकोणम में बीता था जो कि अपने प्राचीन मंदिरों के लिए जाना जाता है। बचपन में रामानुजन का बौद्धिक विकास सामान्य बालकों जैसा नहीं था। यह तीन वर्ष की आयु तक बोलना भी नहीं सीख पाए थे। जब इतनी बड़ी आयु तक जब रामानुजन ने बोलना आरंभ नहीं किया तो सबको चिंता हुई कि कहीं यह गूंगे तो नहीं हैं। बाद के वर्षों में जब उन्होंने विद्यालय में प्रवेश लिया तो भी पारंपरिक शिक्षा में इनका कभी भी मन नहीं लगा। रामानुजन ने दस वर्षों की आयु में प्राइमरी परीक्षा में पूरे जिले में सबसे अधिक अंक प्राप्त किया और आगे की शिक्षा के लिए टाउन हाईस्कूल पहुंचे। रामानुजन को प्रश्न पूछना बहुत पसंद था। उनके प्रश्न अध्यापकों को कभी-कभी बहुत अटपटे लगते थे। जैसे कि-संसार में पहला पुरुष कौन था? पृथ्वी और बादलों के बीच की दूरी कितनी होती है? रामानुजन का व्यवहार बड़ा ही मधुर था। इनका सामान्य से कुछ अधिक स्थूल शरीर और जिज्ञासा से चमकती आखें इन्हें एक अलग ही पहचान देती थीं। इनके सहपाठियों के अनुसार इनका व्यवहार इतना सौम्य था कि कोई इनसे नाराज हो ही नहीं सकता था। विद्यालय में इनकी प्रतिभा ने दूसरे विद्यार्थियों और शिक्षकों पर छाप छोड़ना आरंभ कर दिया। इन्होंने स्कूल के समय में ही कालेज के स्तर के गणित को पढ़ लिया था। एक बार इनके विद्यालय के प्रधानाध्यापक ने यह भी कहा था कि विद्यालय में होने वाली परीक्षाओं के मापदंड रामानुजन के लिए लागू नहीं होते हैं। हाईस्कूल की परीक्षा उत्तीर्ण करने के बाद इन्हें गणित और अंग्रेजी मे अच्छे अंक लाने के कारण सुब्रमण्यम छात्रवृत्ति मिली और आगे कालेज की शिक्षा के लिए प्रवेश भी मिला।

आगे एक परेशानी आई। रामानुजन का गणित के प्रति प्रेम इतना बढ़ गया था कि वे दूसरे विषयों पर ध्यान ही नहीं देते थे। यहां तक की वे इतिहास, जीव विज्ञान की कक्षाओं में भी गणित के प्रश्नों को हल किया करते थे। नतीजा यह हुआ कि ग्यारहवीं कक्षा की परीक्षा में वे गणित को छोड़ कर बाकी सभी विषयों में फेल हो गए और परिणामस्वरूप उनको छात्रवृत्ति मिलनी बंद हो गई। एक तो घर की आर्थिक स्थिति खराब और ऊपर से छात्रवृत्ति भी नहीं मिल रही थी। रामानुजन के लिए यह बड़ा ही कठिन समय था। घर की स्थिति सुधारने के लिए इन्होने गणित के कुछ ट्यूशन तथा खाते-बही का काम भी किया। कुछ समय बाद 1907 में रामानुजन ने फिर से बारहवीं कक्षा की प्राइवेट परीक्षा दी और अनुत्तीर्ण हो गए। और इसी के साथ इनके पारंपरिक शिक्षा की इतिश्री हो गई।

रामानुजन का पैत्रिक आवास

औपचारिक शिक्षा की समाप्ति और संघर्ष का समय

विद्यालय छोड़ने के बाद का पांच वर्षों का समय इनके लिए बहुत हताशा भरा था। भारत इस समय परतंत्रता की बेड़ियों में जकड़ा था। चारों तरफ भयंकर गरीबी थी। ऐसे समय में रामानुजन के पास न कोई नौकरी थी और न ही किसी संस्थान अथवा प्रोफेसर के साथ काम करने का मौका। बस उनका ईश्वर पर अटूट विश्वास और गणित के प्रति अगाध श्रद्धा ने उन्हें कर्तव्य मार्ग पर चलने के लिए सदैव प्रेरित किया। नामगिरी देवी रामानुजन के परिवार की ईष्ट देवी थीं। उनके प्रति अटूट विश्वास ने उन्हें कहीं रुकने नहीं दिया और वे इतनी विपरीत परिस्थितियों में भी गणित के अपने शोध को चलाते रहे। इस समय रामानुजन को ट्यूशन से कुल पांच रूपये मासिक मिलते थे और इसी में गुजारा होता था। रामानुजन का यह जीवन काल बहुत कष्ट और दुःख से भरा था। इन्हें हमेशा अपने भरण-पोषण के लिए और अपनी शिक्षा को जारी रखने के लिए इधर उधर भटकना पड़ा और अनेक लोगों से असफल याचना भी करनी पड़ी।

विवाह और गणित साधना

वर्ष 1908 में इनके माता पिता ने इनका विवाह जानकी नामक कन्या से कर दिया। विवाह हो जाने के बाद अब इनके लिए सब कुछ भूल कर गणित में डूबना संभव नहीं था। अतः वे नौकरी की तलाश में मद्रास आए। बारहवीं की परीक्षा उत्तीर्ण न होने की वजह से इन्हें नौकरी नहीं मिली और उनका स्वास्थ्य भी बुरी तरह गिर गया। अब डॉक्टर की सलाह पर इन्हें वापस अपने घर कुंभकोणम लौटना पड़ा। बीमारी से ठीक होने के बाद वे वापस मद्रास आए और फिर से नौकरी की तलाश शुरू कर दी। ये जब भी किसी से मिलते थे तो उसे अपना एक रजिस्टर दिखाते थे। इस रजिस्टर में इनके द्वारा गणित में किए गए सारे कार्य होते थे। इसी समय किसी के कहने पर रामानुजन वहां के डिप्टी कलेक्टर श्री वी. रामास्वामी अय्यर से मिले। अय्यर गणित के बहुत बड़े विद्वान थे। यहां पर श्री अय्यर ने रामानुजन की प्रतिभा को पहचाना और जिलाधिकारी श्री रामचंद्र राव से कह कर इनके लिए 25 रूपये मासिक छात्रवृत्ति का प्रबंध भी कर दिया। इस वृत्ति पर रामानुजन ने मद्रास में एक साल रहते हुए अपना प्रथम शोधपत्र प्रकाशित किया। शोध पत्र का शीर्षक था "बरनौली संख्याओं के कुछ गुण” और यह शोध पत्र जर्नल ऑफ इंडियन मैथेमेटिकल सोसाइटी में प्रकाशित हुआ था। यहां एक साल पूरा होने पर इन्होने मद्रास पोर्ट ट्रस्ट में क्लर्क की नौकरी की। सौभाग्य से इस नौकरी में काम का बोझ कुछ ज्यादा नहीं था और यहां इन्हें अपने गणित के लिए पर्याप्त समय मिलता था। यहां पर रामानुजन रात भर जाग कर नए-नए गणित के सूत्र लिखा करते थे और फिर थोड़ी देर तक आराम कर के फिर दफ्तर के लिए निकल जाते थे। रामानुजन गणित के शोधों को स्लेट पर लिखते थे। और बाद में उसे एक रजिस्टर में लिख लेते थे। रात को रामानुजन के स्लेट और खड़िए की आवाज के कारण परिवार के अन्य सदस्यों की नींद चौपट हो जाती थी।

प्रोफेसर हार्डी के साथ पत्रव्यावहार

इस समय भारतीय और पश्चिमी रहन सहन में एक बड़ी दूरी थी और इस वजह से सामान्यतः भारतीयों को अंग्रेज वैज्ञानिकों के सामने अपने बातों को प्रस्तुत करने में काफी संकोच होता था। इधर स्थिति कुछ ऐसी थी कि बिना किसी अंग्रेज गणितज्ञ की सहायता लिए शोध कार्य को आगे नहीं बढ़ाया जा सकता था। इस समय रामानुजन के पुराने शुभचिंतक इनके काम आए और इन लोगों ने रामानुजन द्वारा किए गए कार्यों को लंदन के प्रसिद्ध गणितज्ञों के पास भेजा। पर यहां इन्हें कुछ विशेष सहायता नहीं मिली लेकिन एक लाभ यह हुआ कि लोग रामानुजन को थोड़ा बहुत जानने लगे थे। इसी समय रामानुजन ने अपने संख्या सिद्धांत के कुछ सूत्र प्रोफेसर शेषू अय्यर को दिखाए तो उनका ध्यान लंदन के ही प्रोफेसर हार्डी की तरफ गया। प्रोफेसर हार्डी उस समय के विश्व के प्रसिद्ध गणितज्ञों में से एक थे। और अपने सख्त स्वभाव और अनुशासन प्रियता के कारण जाने जाते थे। प्रोफेसर हार्डी के शोधकार्य को पढ़ने के बाद रामानुजन ने बताया कि उन्होने प्रोफेसर हार्डी के अनुत्तरित प्रश्न का उत्तर खोज निकाला है। अब रामानुजन का प्रोफेसर हार्डी से पत्रव्यवहार आरंभ हुआ। अब यहां से रामानुजन के जीवन में एक नए युग का सूत्रपात हुआ जिसमें प्रोफेसर हार्डी की बहुत बड़ी भूमिका थी। दूसरे शब्दों में कहा जाए तो जिस तरह से एक जौहरी हीरे की पहचान करता है और उसे तराश कर चमका देता है, रामानुजन के जीवन में वैसा ही कुछ स्थान प्रोफेसर हार्डी का है। प्रोफेसर हार्डी आजीवन रामानुजन की प्रतिभा और जीवन दर्शन के प्रशंसक रहे। रामानुजन और प्रोफेसर हार्डी की यह मित्रता दोनो ही के लिए लाभप्रद सिद्ध हुई। एक तरह से देखा जाए तो दोनो ने एक दूसरे के लिए पूरक का काम किया। प्रोफेसर हार्डी ने उस समय के विभिन्न प्रतिभाशाली व्यक्तियों को 100 के पैमाने पर आंका था। अधिकांश गणितज्ञों को उन्होने 100 में 35 अंक दिए और कुछ विशिष्ट व्यक्तियों को 60 अंक दिए। लेकिन उन्होंने रामानुजन को 100 में पूरे 100 अंक दिए थे।

आरंभ में रामानुजन ने जब अपने किए गए शोधकार्य को प्रोफेसर हार्डी के पास भेजा तो पहले उन्हें भी पूरा समझ में नहीं आया। जब उन्होंने अपने मित्र गणितज्ञों से सलाह ली तो वे इस निष्कर्ष पर पहुंचे कि रामानुजन गणित के क्षेत्र में एक दुर्लभ व्यक्तित्व है और इनके द्वारा किए गए कार्य को ठीक से समझने और उसमें आगे शोध के लिए उन्हें इंग्लैंड आना चाहिए। अतः उन्होने रामानुजन को कैंब्रिज आने के लिए आमंत्रित किया।

विदेश गमन

कुछ व्यक्तिगत कारणों और धन की कमी के कारण रामानुजन ने प्रोफेसर हार्डी के कैंब्रिज के आमंत्रण को अस्वीकार कर दिया। प्रोफेसर हार्डी को इससे निराशा हुई लेकिन उन्होनें किसी भी तरह से रामानुजन को वहां बुलाने का निश्चय किया। इसी समय रामानुजन को मद्रास विश्वविद्यालय में शोध वृत्ति मिल गई थी जिससे उनका जीवन कुछ सरल हो गया और उनको शोधकार्य के लिए पूरा समय भी मिलने लगा था। इसी बीच एक लंबे पत्रव्यवहार के बाद धीरे-धीरे प्रोफेसर हार्डी ने रामानुजन को कैंब्रिज आने के लिए सहमत कर लिया। प्रोफेसर हार्डी के प्रयासों से रामानुजन को कैंब्रिज जाने के लिए आर्थिक सहायता भी मिल गई। रामानुजन ने इंग्लैण्ड जाने के पहले गणित के करीब 3000 से भी अधिक नये सूत्रों को अपनी नोटबुक में लिखा था।

रामानुजन ने लंदन की धरती पर कदम रखा। वहां प्रोफेसर हार्डी ने उनके लिए पहले से व्ववस्था की हुई थी अतः इन्हें कोई विशेष परेशानी नहीं हुई। इंग्लैण्ड में रामानुजन को बस थोड़ी परेशानी थी और इसका कारण था उनका शर्मीला, शांत स्वभाव और शुद्ध सात्विक जीवनचर्या। अपने पूरे इंग्लैण्ड प्रवास में वे अधिकांशतः अपना भोजन स्वयं बनाते थे। इंग्लैण्ड की इस यात्रा से उनके जीवन में क्रांतिकारी परिवर्तन आया। उन्होंने प्रोफेसर हार्डी के साथ मिल कर उच्चकोटि के शोधपत्र प्रकाशित किए। अपने एक विशेष शोध के कारण इन्हें कैंब्रिज विश्वविद्यालय द्वारा बी.ए. की उपाधि भी मिली। लेकिन वहां की जलवायु और रहन-सहन की शैली उनके अधिक अनुकूल नहीं थी और उनका स्वास्थ्य खराब रहने लगा। डॉक्टरों ने इसे क्षय रोग बताया। उस समय क्षय रोग की कोई दवा नहीं होती थी और रोगी को सेनेटोरियम मे रहना पड़ता था। रामानुजन को भी कुछ दिनों तक वहां रहना पड़ा। वहां इस समय भी यह गणित के सूत्रों में नई नई कल्पनाएं किया करते थे।

रॉयल सोसाइटी की सदस्यता

इसके बाद वहां रामानुजन को रॉयल सोसाइटी का फेलो नामित किया गया। ऐसे समय में जब भारत गुलामी में जी रहा था तब एक अश्वेत व्यक्ति को रॉयल सोसाइटी की सदस्यता मिलना एक बहुत बड़ी बात थी। रॉयल सोसाइटी के पूरे इतिहास में इनसे कम आयु का कोई सदस्य आज तक नहीं हुआ है। पूरे भारत में उनके शुभचिंतकों ने उत्सव मनाया और सभाएं की। रॉयल सोसाइटी की सदस्यता के बाद यह ट्रिनीटी कॉलेज की फेलोशिप पाने वाले पहले भारतीय भी बने। अब ऐसा लग रहा था कि सब कुछ बहुत अच्छी जगह पर जा रहा है। लेकिन रामानुजन का स्वास्थ्य गिरता जा रहा था और अंत में डॉक्टरों की सलाह पर उन्हें वापस भारत लौटना पड़ा। भारत आने पर इन्हें मद्रास विश्वविद्यालय में प्राध्यापक की नौकरी मिल गई। और रामानुजन अध्यापन और शोध कार्य में पुनः रम गए।

स्वदेश आगमन

भारत लौटने पर भी स्वास्थ्य ने इनका साथ नहीं दिया और हालत गंभीर होती जा रही थी। इस बीमारी की दशा में भी इन्होने मॉक थीटा फंक्शन पर एक उच्च स्तरीय शोधपत्र लिखा। रामानुजन द्वारा प्रतिपादित इस फलन का उपयोग गणित ही नहीं बल्कि चिकित्साविज्ञान में कैंसर को समझने के लिए भी किया जाता है।

मृत्यु

इनका गिरता स्वास्थ्य सबके लिए चिंता का विषय बन गया और यहां तक की अब डॉक्टरों ने भीजवाब दे दिया था। अंत में रामानुजन के विदा की घड़ी आ ही गई। 26 अप्रैल1920 के प्रातः काल में वे अचेत हो गए और दोपहर होते होते उन्होने प्राण त्याग दिए। इस समय रामानुजन की आयु मात्र 33 वर्ष थी। इनका असमय निधन गणित जगत के लिए अपूरणीय क्षति था। पूरे देश विदेश में जिसने भी रामानुजन की मृत्यु का समाचार सुना वहीं स्तब्ध हो गया।

रामानुजन की कार्यशैली और शोध

रामानुजन और इनके द्वारा किए गए अधिकांश कार्य अभी भी वैज्ञानिकों के लिए अबूझ पहेली बने हुए हैं। एक बहुत ही सामान्य परिवार में जन्म ले कर पूरे विश्व को आश्चर्यचकित करने की अपनी इस यात्रा में इन्होने भारत को अपूर्व गौरव प्रदान किया। इनका उनका वह पुराना रजिस्टर जिस पर वे अपने प्रमेय और सूत्रों को लिखा करते थे 1976 में अचानक ट्रिनीटी कॉलेज के पुस्तकालय में मिला। करीब एक सौ पन्नों का यह रजिस्टर आज भी वैज्ञानिकों के लिए एक पहेली बना हुआ है। इस रजिस्टर को बाद में रामानुजन की नोट बुक के नाम से जाना गया। मुंबई के टाटा मूलभूत अनुसंधान संस्थान द्वारा इसका प्रकाशन भी किया गया है। रामानुजन के शोधों की तरह उनके गणित में काम करने की शैली भी विचित्र थी। वे कभी कभी आधी रात को सोते से जाग कर स्लेट पर गणित से सूत्र लिखने लगते थे और फिर सो जाते थे। इस तरह ऐसा लगता था कि वे सपने में भी गणित के प्रश्न हल कर रहे हों। रामानुजन के नाम के साथ ही उनकी कुलदेवी का भी नाम लिया जाता है। इन्होने शून्य और अनन्त को हमेशा ध्यान में रखा और इसके अंतर्सम्बन्धों को समझाने के लिए गणित के सूत्रों का सहारा लिया। रामानुजन के कार्य करने की एक विशेषता थी। पहले वे गणित का कोई नया सूत्र या प्रमेंय पहले लिख देते थे लेकिन उसकी उपपत्ति पर उतना ध्यान नहीं देते थे। इसके बारे में पूछे जाने पर वे कहते थे कि यह सूत्र उन्हें नामगिरी देवी की कृपा से प्राप्त हुए हैं। रामानुजन का आध्यात्म के प्रति विश्वास इतना गहरा था कि वे अपने गणित के क्षेत्र में किये गए किसी भी कार्य को आध्यात्म का ही एक अंग मानते थे। वे धर्म और आध्यात्म में केवल विश्वास ही नहीं रखते थे बल्कि उसे तार्किक रूप से प्रस्तुत भी करते थे। वे कहते थे कि "मेरे लिए गणित के उस सूत्र का कोई मतलब नहीं है जिससे मुझे आध्यात्मिक विचार न मिलते हों।”

गणितीय कार्य एवं उपलब्धियाँ

रामानुजन ने इंग्लैण्ड में पाँच वर्षों तक मुख्यतः samkhya sidhant के क्षेत्र में काम किया।

सूत्र

रामानुजन् ने निम्नलिखित सूत्र प्रतिपादित किया-

${\displaystyle 1+{\frac {1}{1\cdot 3}}+{\frac {1}{1\cdot 3\cdot 5}}+{\frac {1}{1\cdot 3\cdot 5\cdot 7}}+{\frac {1}{1\cdot 3\cdot 5\cdot 7\cdot 9}}+\cdots +{1 \over 1+{1 \over 1+{2 \over 1+{3 \over 1+{4 \over 1+{5 \over 1+\cdots }}}}}}={\sqrt {\frac {e\cdot \pi }{2}}}}$

इस सूत्र की विशेषता यह है कि यह गणित के दो सबसे प्रसिद्ध नियतांकों ('पाई' तथा 'ई') का सम्बन्ध एक anant satat finn के माध्यम से व्यक्त करता है।

पाई के लिये उन्होने एक दूसरा सूत्र भी (सन् १९१० में) दिया था-

${\displaystyle \pi ={\frac {9801}{2{\sqrt {2}}\displaystyle \sum _{n=0}^{\infty }{\frac {(4n)!}{(n!)^{4}}}\times {\frac {[1103+26390n]}{(4\times 99)^{4n}}}}}}$

रामानुजन संख्याएँ

'रामानुजन संख्या' उसprakrtik snkhya को कहते हैं जिसे दो अलग-अलग प्रकार से दो संख्याओं के घनों के योग द्वारा निरूपित किया जा सकता है।

उदाहरण -.

इसी प्रकार,

@jeegarsaini

• ${\displaystyle 2^{3}+16^{3}=9^{3}+15^{3}=4104}$
• ${\displaystyle 10^{3}+27^{3}=19^{3}+24^{3}=20683}$
• ${\displaystyle 2^{3}+34^{3}=15^{3}+33^{3}=39312}$
• ${\displaystyle 9^{3}+34^{3}=16^{3}+33^{3}=40033}$

अतः 1729, 4104, 20683, 39312, 40033  आदि रामानुजन संख्याएं हैं।

पायथागोरस प्रमेय

पायथागोरस प्रमेय  
गणित में, पायथागोरस  प्रमेय समकोण  त्रिभुज (सम-कोण त्रिभुज) की तीनों  भुजाओं के बीच  यूक्लिडियन  ज्यामिति में एक संबंध है।

क्षेत्रफल के अर्थ में, यह बताता है : किसी भी समकोण त्रिभुज में, उस वर्ग का क्षेत्रफल जिसकी भुजा कर्ण है (समकोण की सम्मुख भुजा), उन वर्गों के क्षेत्रफलों के योगफल के बराबर होता है जिनकी भुजाएं दो पाद (लेग) (समकोण पर मिलने वाली दो भुजाएं) होती हैं।
                                                                                        or
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाओ के वर्गो का योग तीसरी   भुजा के वर्ग के बराबर होता है
AB²=BC²+CA²

पाइथागोरस प्रमेय

                                                                         
                                                                                                              चित्र( १ )

प्रमेय को भुजाओं a, b और c की लंबाइयों के बीच संबंध बनाते हुए समीकरण के रूप में लिखा जा सकता है, जिसे पायथागोरस समीकरण a^2+b^2=c^2 कहते हैं। जहां c कर्ण की लंबाई को दर्शाता है, और a तथा b अन्य दो भुजाओं की लंबाइयों को दर्शाता है।

उदाहरण :-

दिए गए समकोण त्रिभुज ABC में AB की लंबाई कितनी है?
पायथागोरस प्रमेय द्वारा, हम देखते हैं :
AB²=BC²+CA²

गोले का आयतन

गोले का आयतन

उद्देश्य :

 गोले की त्रिज्या के पदों में इसके आयतन के सूत्र का एक सांकेतिक नमूना प्रदान करना।

 

संबंधित शब्दावलियां

गोला :

                                                                                                               

                                                                          

गोला एक पूरी तरह से गोल ज्यामितीय और वृत्ताकार वस्तु है जो त्रि-आयामी फैलाव में होता है और जो संपूर्ण रूप से गोल गेंद की तरह दिखाई देता है।  

व्यास :  

व्यास एक सीधी रेखा होती है जो वृत्त या गोले के केंद्र से गुजरती है और प्रत्येक सिरे पर परिधि अथवा सतह से मिलती है।  

त्रिज्या :  

किसी गोले की त्रिज्या केंद्र और वृत्त या गोले पर स्थित किसी बिंदु के बीच एक रेखाखंड होती है।  

आयतन : 

गोले के आयतन को निम्न अनुसार परिभाषित किया जाता है :  V = ⁴⁄₃πr³.

इस समीकरण में "V” आयतन को और "r” गोले की त्रिज्या को निरूपित करता है।

समांतर चतुर्भुज की विशेषताएं

समांतर चतुर्भुज की विशेषताए

उद्देश्य :

समचतुर्भुज के विकर्णों से संबंधित विशेषता में समानताओं और भिन्नताओं का पता लगाना। 

समांतर चतुर्भुज

परिभाषा

यह वह चतुर्भुज है जिसमें सम्मुख भुजाओं के दोनों युग्म समांतर होते हैं। चतुर्भुज ABCD एक समांतर चतुर्भुज है।

                                   

विशेषताएं :

किसी समांतर चतुर्भुज का विकर्ण इसे दो सर्वांगसम त्रिभुजों में विभाजित करता है (▲ ADB सर्वांगसम ▲ ABC)।किसी समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।सम्मुख भुजाएं सर्वांगसम होती हैं (AB = DC)।सम्मुख कोण सर्वांगसम होते हैं (∠ADC= ∠ABC)।क्रमागत कोण पूरक होते हैं (∠DAB + ∠ADC = 180°)।यदि एक कोण समकोण हो तो, सभी कोण समकोण होते हैं।