From the day I learned Calculus, I noticed that I had become obsessed with learning how certain things worked. While it is fun to understand how certain things work, it is even more entertaining to learn about how something was discovered. Furthermore, it is most amusing to learn how something works or exists on our own. For example, knowing that 2•2=4 isn’t very rewarding for a child. However, understanding why 2•2=4, demonstrating it with wooden blocks, is extremely rewarding.
That is why it is so enjoyable to come up with and read about proofs. To write out a proof takes skill outside of coming up with it. Many times, brilliant people struggle to write out why certain things are the way they are. Putting into writing a certain proof should have its own education. Sadly, schools don’t teach students about proofs, what they are, and how they are come up with. I genuinely hope this will get mended soon. If you want to learn how to fabricate proofs, I suggest you read ‘How to solve it’ by George Polya.
First of all, I would like to mention that the person who first proved the theorem I will demonstrate below didn’t stumble upon it accidentally. He discovered this truth because he is a brilliant individual. Furthermore, he performed this with a few fundamental trigonometric ideas. That shows that you can also find beautiful mathematical proofs and truths with a simple amount of knowledge.
We must remember that just because one person has proved a theorem doesn’t mean that you can’t verify it independently as well. If you can prove said theorem sitting at home, that theorem now belongs to you. It doesn’t matter whether the rest of the world acknowledges it as your theorem.
I saw a very famous theorem amongst AP Calculus students on Khan Academy. I will unravel its proof step-by-step below and it may seem complicated to some but is quite simple. Mathematicians like proofs to be simplified and clean. The fact that there are many writings and equations never shadows the beauty of the proof. This proof may be long-winded, but this is because I have tried to provide details about every piece of information. If you near the middle of the proof and don’t still understand it, please don’t panic. You need to read a little more carefully.
Claim: The limit of sin(x)/x as x approaches 0 is 1.To build the proof, we will begin by making some trigonometric constructions. When you think about trigonometry, your mind naturally wanders to the unit circle. By definition, a unit circle is a circle with a radius of 1. To perform trigonometric operations on it, we first divide it into four equal portions.
Unit Circle: The unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane.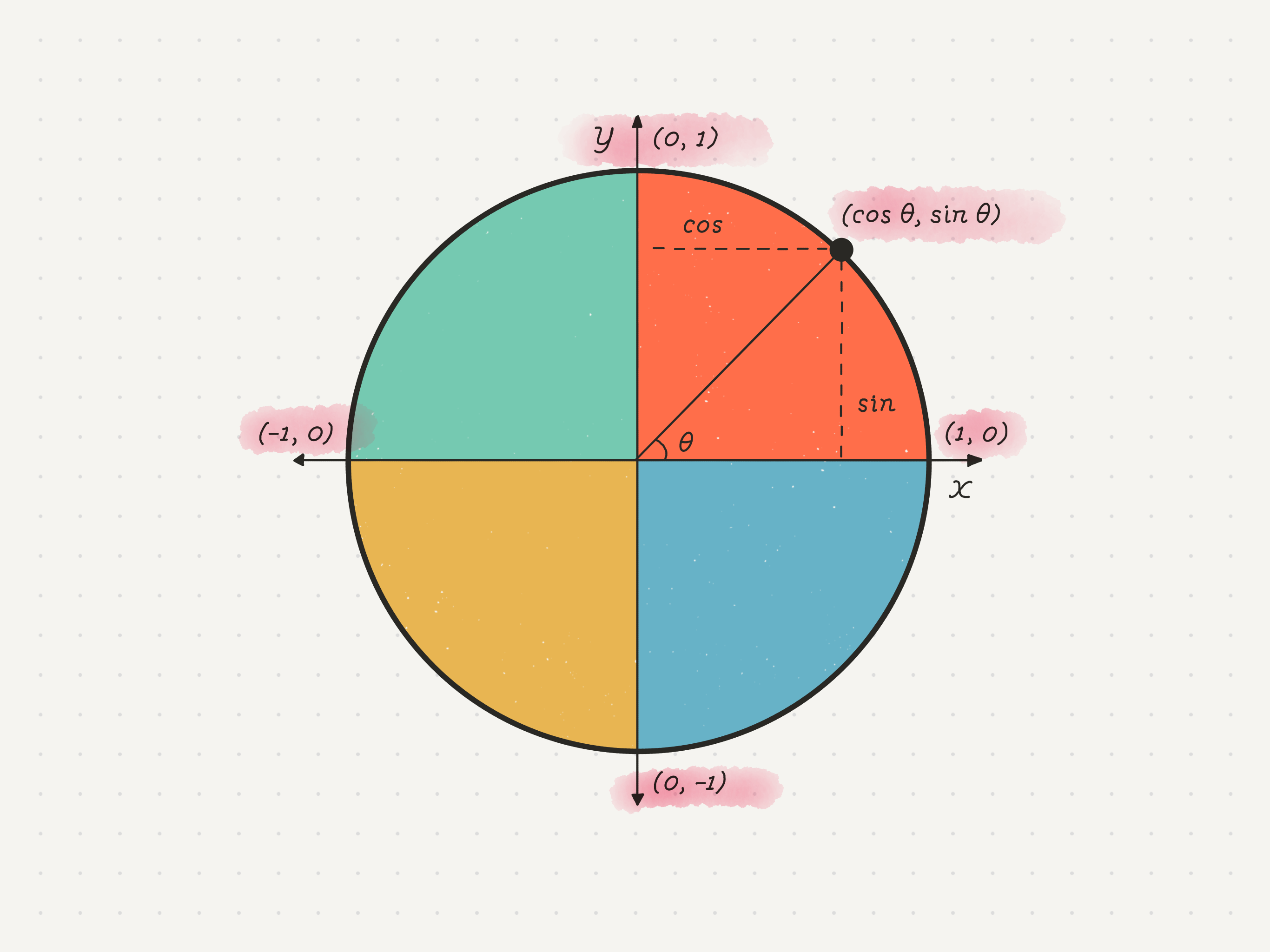
Proof: First, we will build our proof in the first quadrant of the unit circle. To start, let’s make two similar triangles, ABC and ADE. Color the smaller triangle, ABC, green to distinguish it. If you’ll notice, both the triangle’s hypotenuses are on the same line.
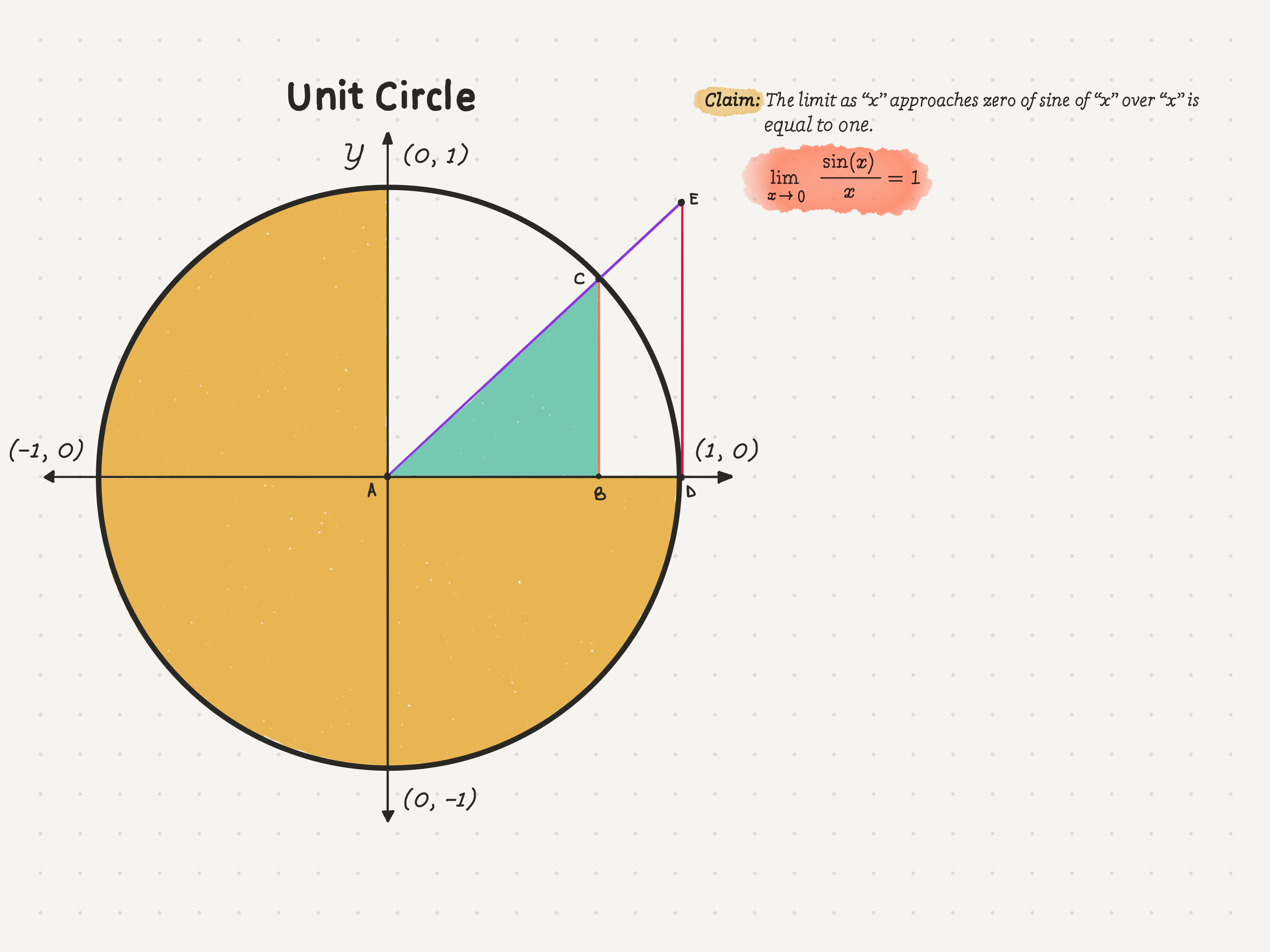
Definition: “Hypotenuse” is the longest side of a right triangle, opposite the right angle.Per definition, the radius of the unit circle is equal to 1. Therefore, the hypotenuse, AC, of the smaller triangle must be 1. Then what is BC equal to? Point C will be at the intersection of the radius we drew and the unit circle, meaning that the length of BC is equal to the y value of point C.
If we wanted to find the sin value of x, by definition, it would have to be sin(x) = BC/1. Therefore, BC = sin(x). It is imperative to remember that while sin(x) is equal to a number since we don’t know the number yet, we define it as sin(x).
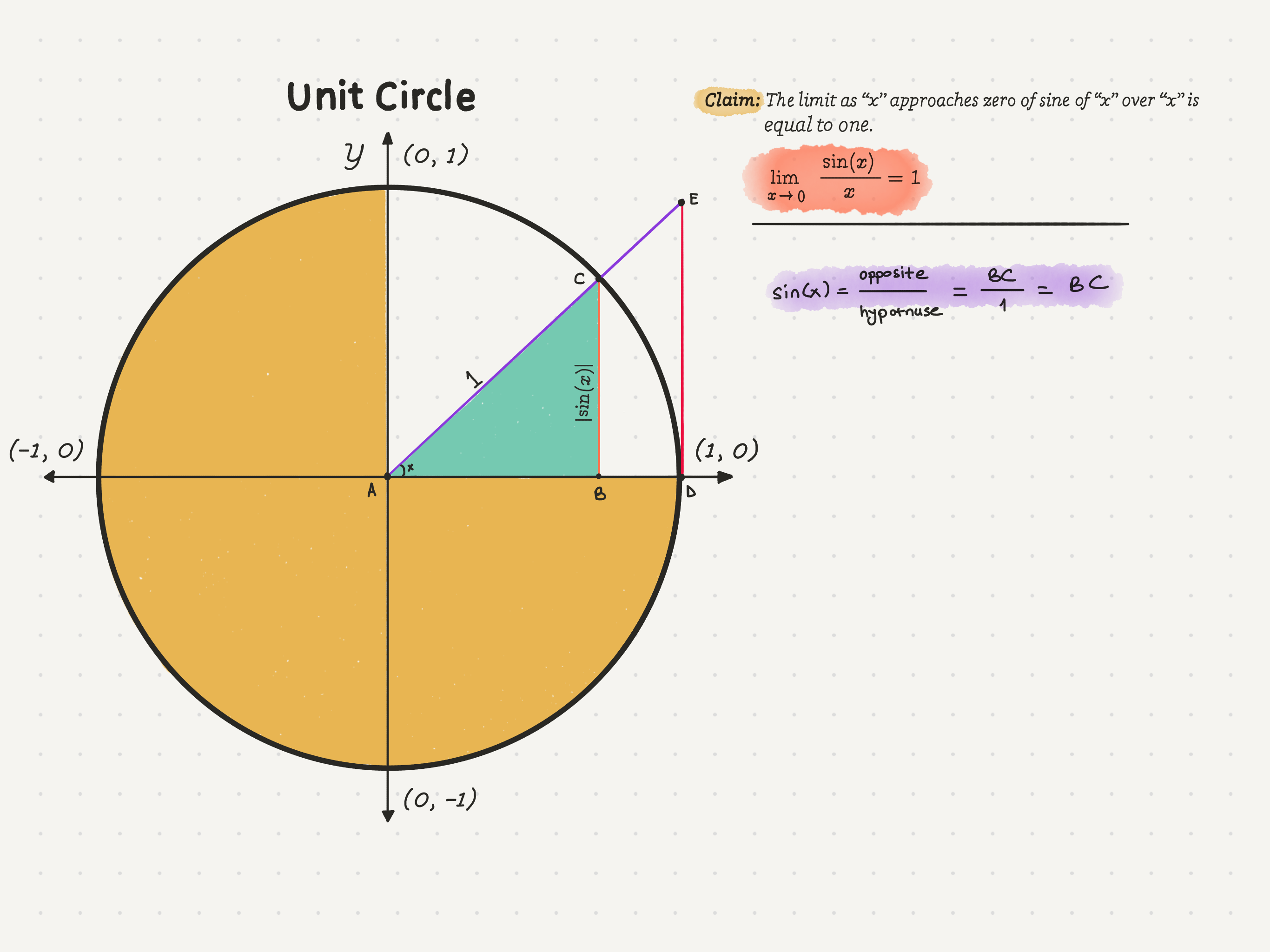
As you can see, we have defined the length of BC using a trigonometric function. If we can do this for the BC side of ABC, we can also use a trigonometric function to define the DE side of ADE.
Since we don’t know the hypotenuse of the triangle ADE, let’s use a different function todefine it. Since the length of AD in the triangle ADE is equal to the radius of the unit circle, it makes sense to use the tangent function. That is because tan(x) is equal to opposite over adjacent. Meaning, tan(x) = DE/1. And since we are working on the unit circle, we get DE = tan(x).Note: The adjacent side is the non-hypotenuse side that is next to a given angle.

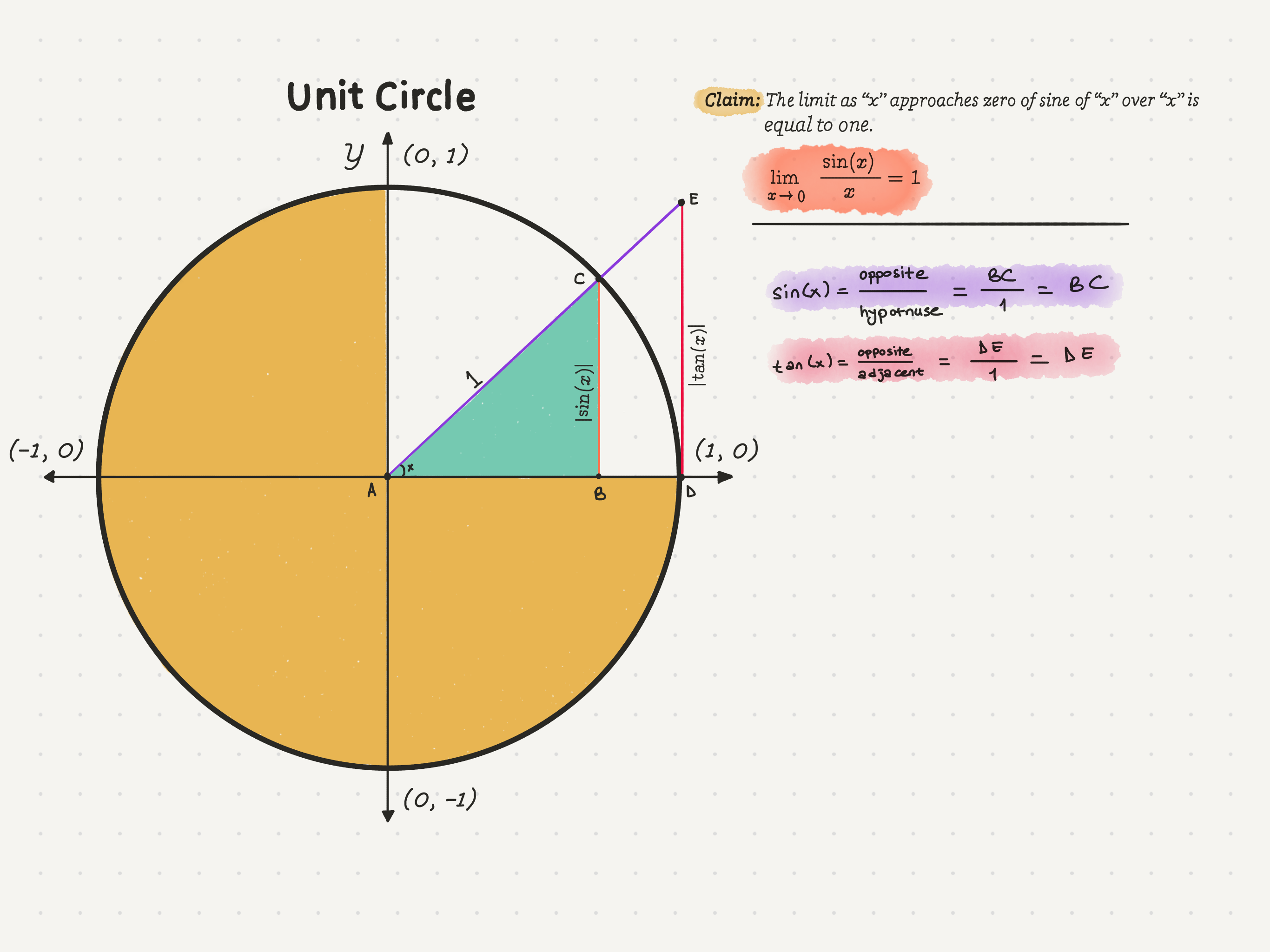
Excellent! We have almost found all of the side lengths. Now, what should we do?
Since we have found almost all side lengths, let’s deal with a little bit of area calculation. To do this, let’s connect the corners C and D with a line and call this new triangle within the circle, triangle ACD. Now we can color the empty space of this triangle blue.
Perfect. Now we can work on the triangle ACD, composed of yellow and blue. How can we represent the area triangle ACD? There is a neat fact that we know regarding triangles; the area of any triangle is half of the product of the base multiplied by the height.
The base length of ACD is equal to 1, as is very clear. The height is equal to BC, and as weconcluded earlier, BC is equal to |sin(x)|. Therefore, the area of triangle ACD is equal to 1•|sin(x)| / 2, or |sin(x)|/2. (Absolute value of sin of x over two)
We have found the area of triangle ACD. Next, we need to find the area of the ACD portion of our circle (green area + blue area + orange area).
We already know how to find the area of a circle. The area of a circle is π times radius square. However, we don’t need the entire area. We only want the green area + blue area + orange area. Therefore, we need to find the ratio of the desired area to the entire area. Here, we can use the following logic.
Note: If we were to go all the way around the circle, it would be 2π radians, right? Therefore, the portion that angle x covers to the entire circle is x/2π.The logic mentioned above will be of utmost use to us as we work on the unit circle. Since the radius of the unit circle is 1, using the πr² formula, we know that the area is just pi. Since if we put one instead of r, 1²=1.
Truth: The area of a unit square is just π.We can now find the area of the ACD portion of the circle. The area of the circle isequal to π, and the ratio of the shaded area to the entire area is x/2π. Therefore, the area of ACD (green area + blue area + orange area) is equal to x/2π * π, or x/2. Furthermore, since the area has to be a positive value, we again use absolute value symbols.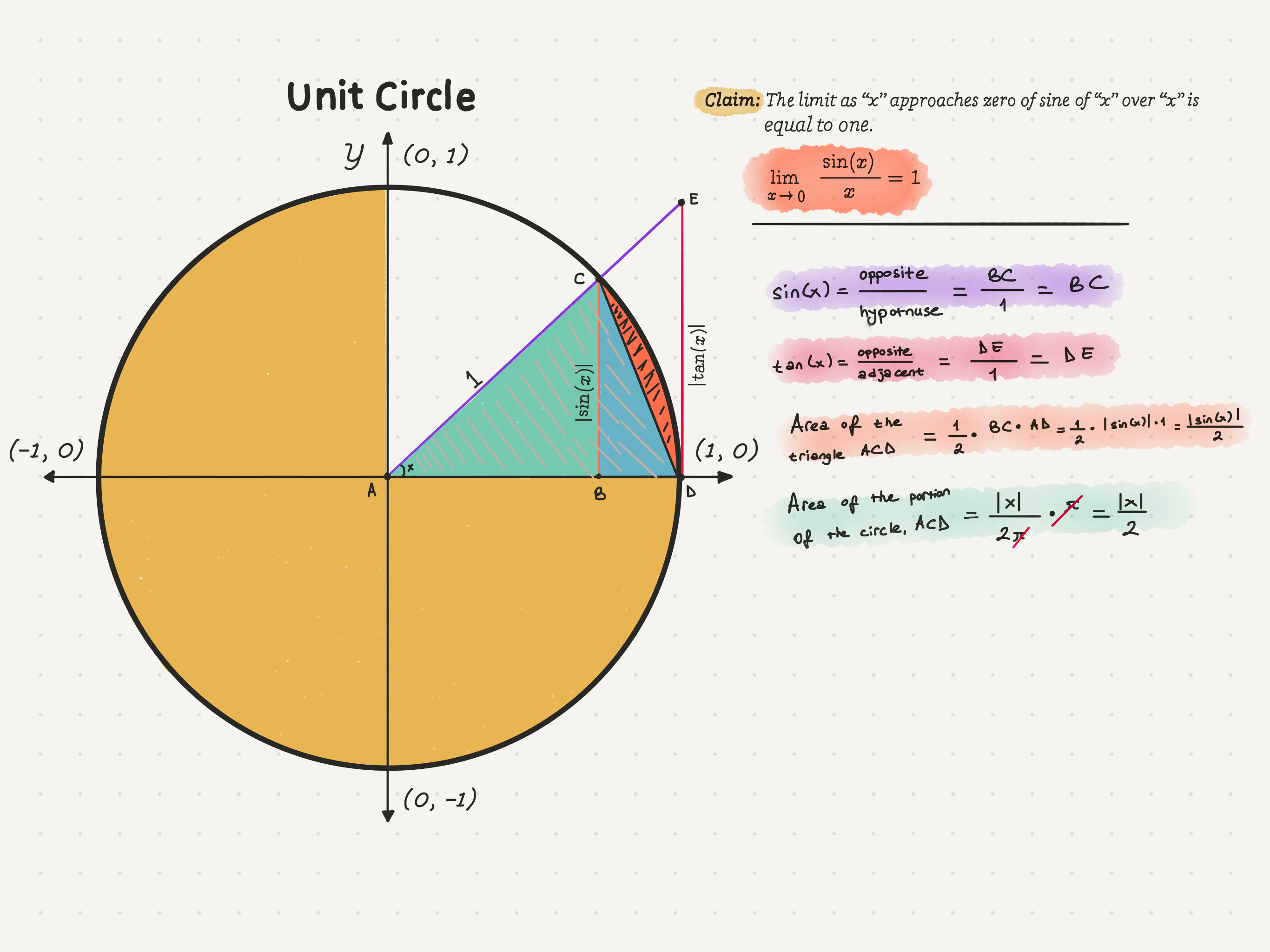
Now we can brainstorm on the area of the largest triangle, triangle ADE. Actually, finding the area is relatively straightforward as all we have to do is divide the product of length AD and length DE by 2. Somewhere above, we found that the length of DE to be |tan(x)|. Since the length of AD is equal to the radius, it is equal to 1. Therefore, the area of triangle ADE is |tan(x)|/2. Perfect!

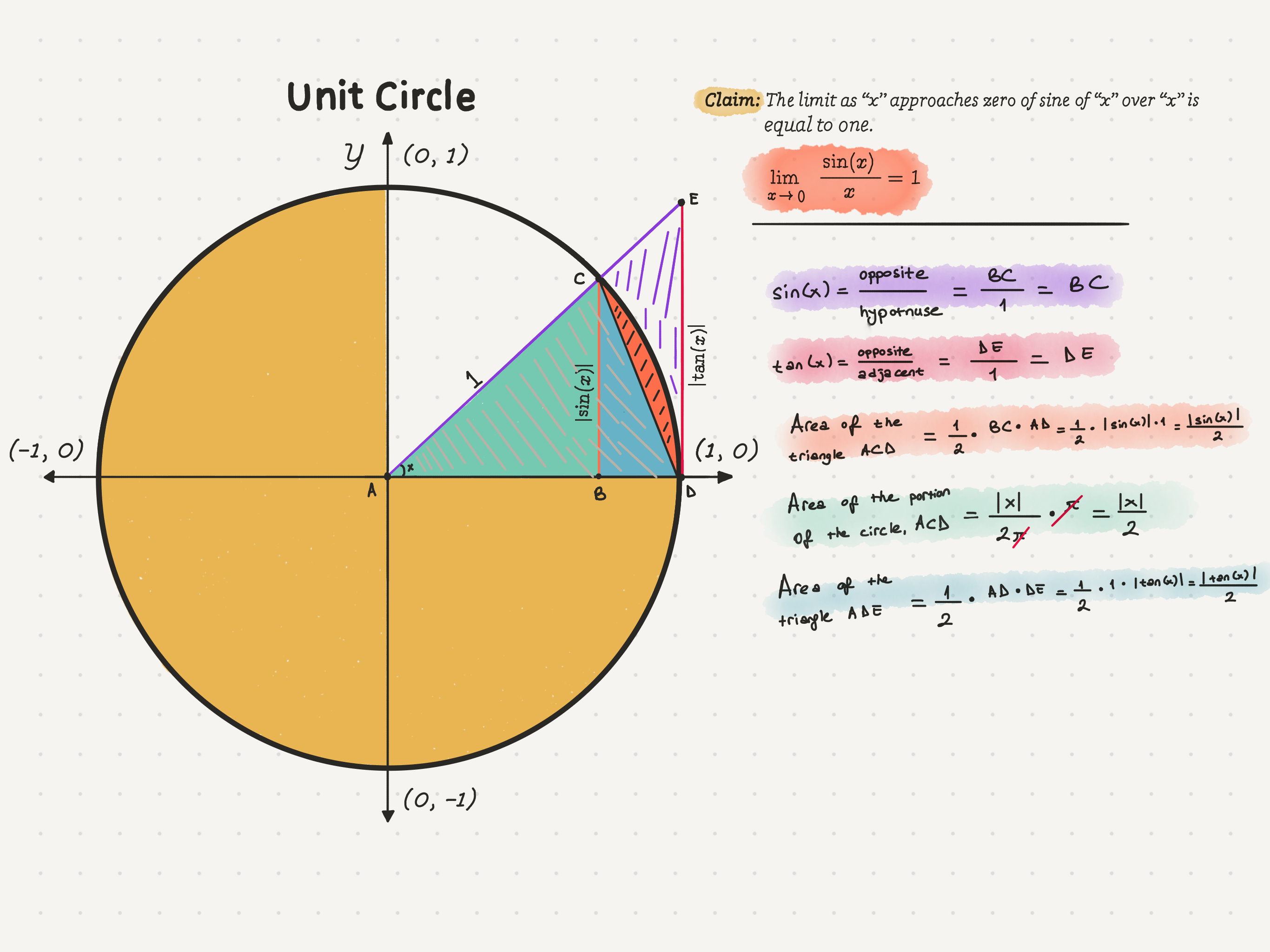
What will we do with these area values, though? We will compare them to each other. How though? We have the areas of triangles ABC, ACD, and ADE, and the ACD portion of the circle that we can compare. As we can see, the area of triangle ACD is less than or equal to the area of the ACD portion of the circle. Furthermore, the circle’s ACD portion is less than or equal to the area of triangle ADE. Therefore,
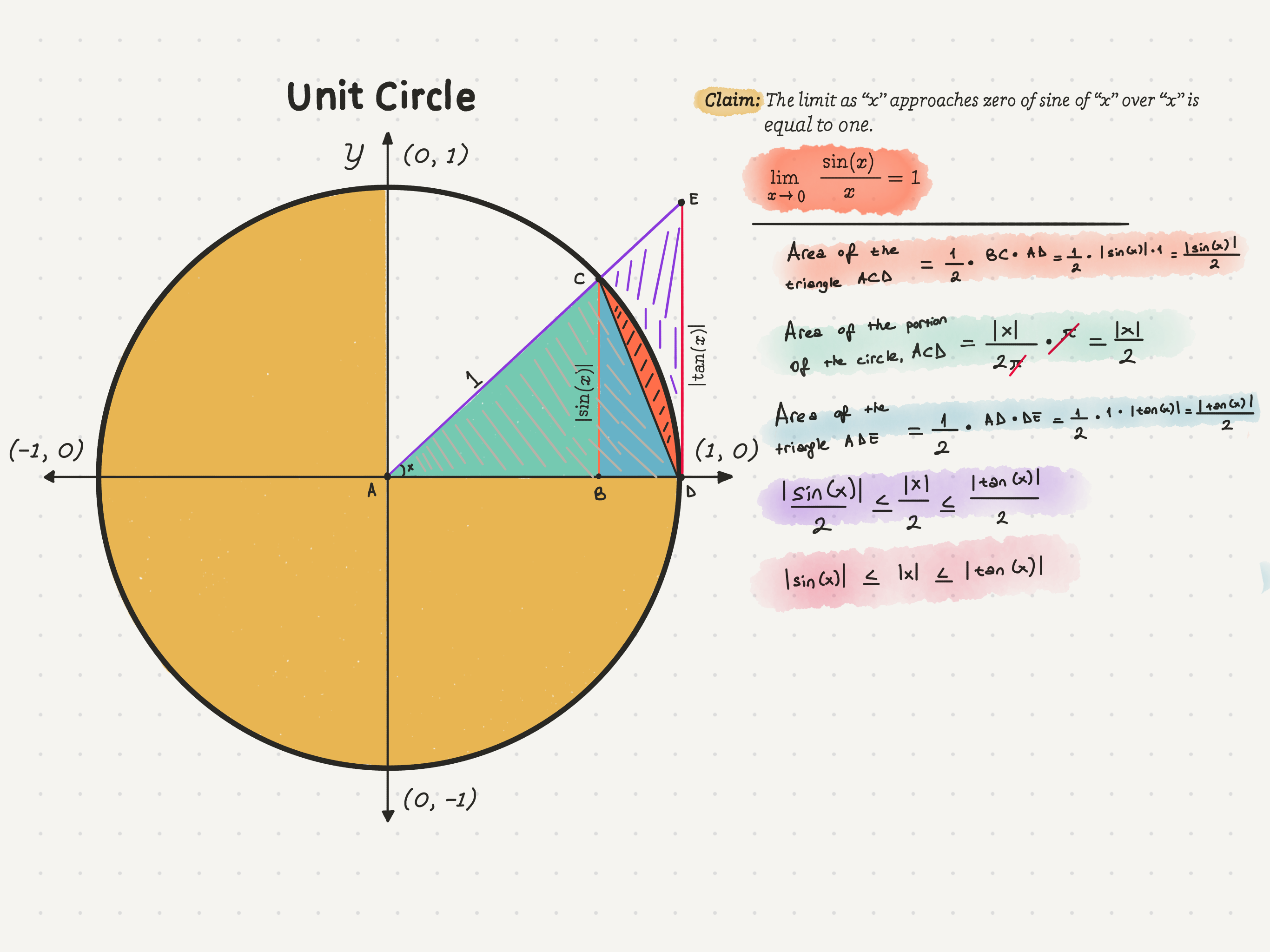
|sin(x)|/2 ≤ x/2 ≤|tan(x)|/2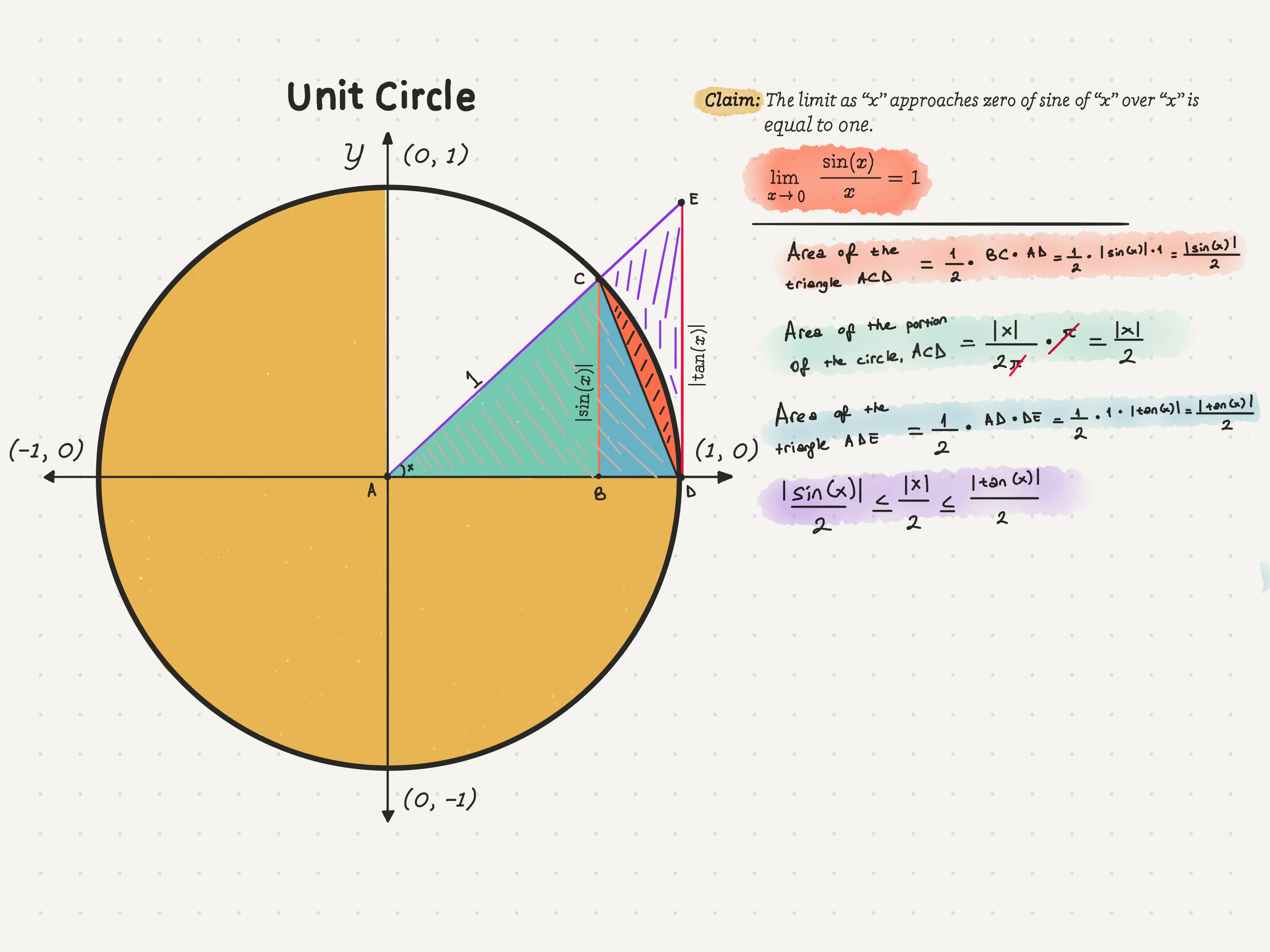
So far, so good. Now, we have to manipulate this inequality a little bit. One thing we have to be wary of, however, is making sure to keep the inequality balanced. For example, instead of 3, we can write 6/2, and it will remain the same.
Since the terms in the inequality are divided by 2, we can multiply them by 2 to eliminate the denominator, simplifying the inequality. That gives us, the absolute value of sin of x is less than or equal to the absolute value of x, which is less than or equal to the absolute value of the tangent of x.
|sin(x)| ≤ x ≤|tan(x)|
At this point, we can manipulate the tangent function and write it differently. That is because the tangent of x is equal to the sin of x over the cosine of x.
|sin(x)| ≤ x ≤ |sin(x)|/|cos(x)|
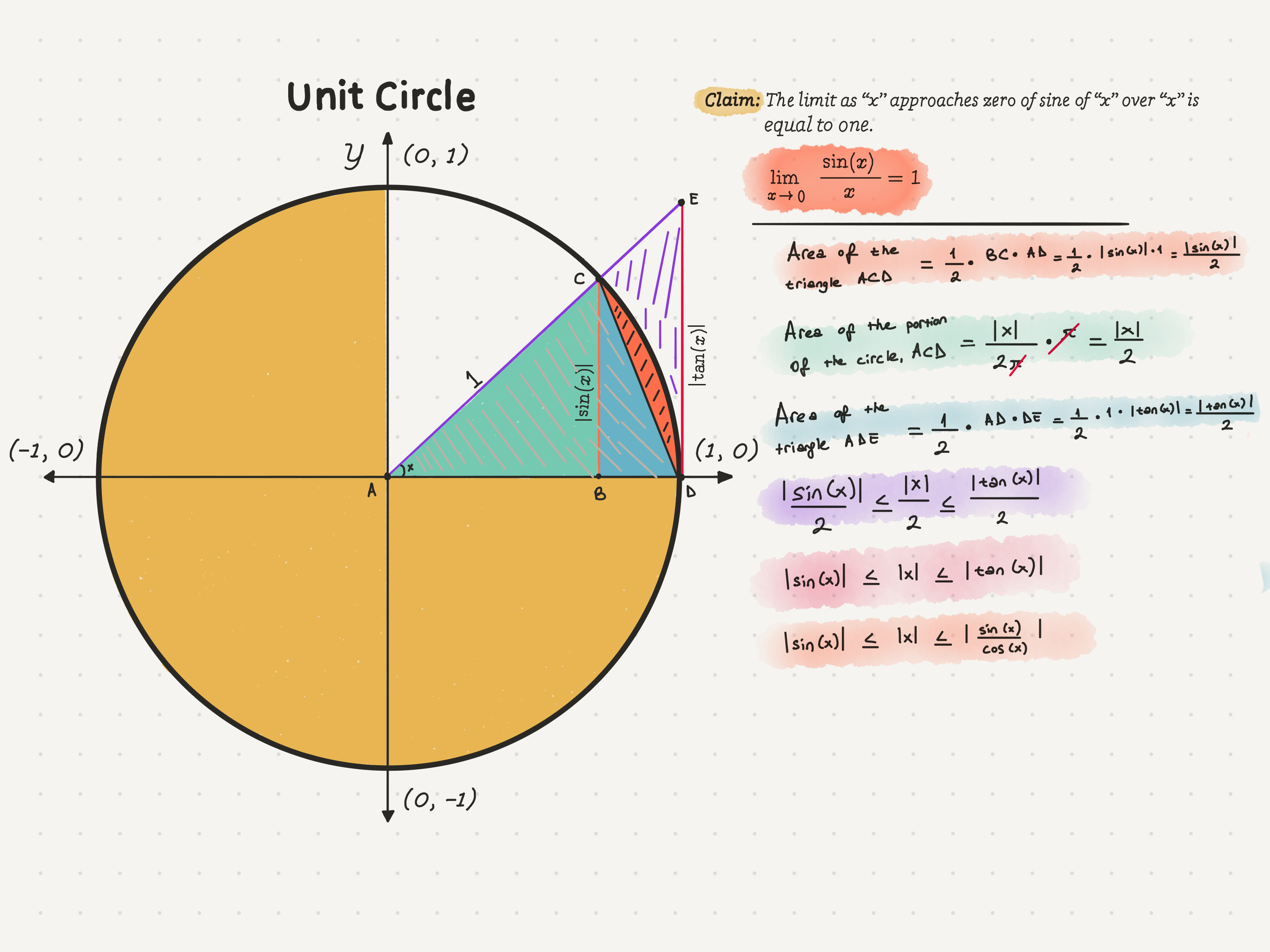
As you can see, we have achieved a very different inequality. However, we need to manipulate the inequality further. We can now divide all of the terms by the absolute value of x. That will result in the following inequality.
|sin(x)|/|sin(x)| ≤ x/|sin(x)| ≤ |sin(x)|/|cos(x)|• 1/|sin(x)|
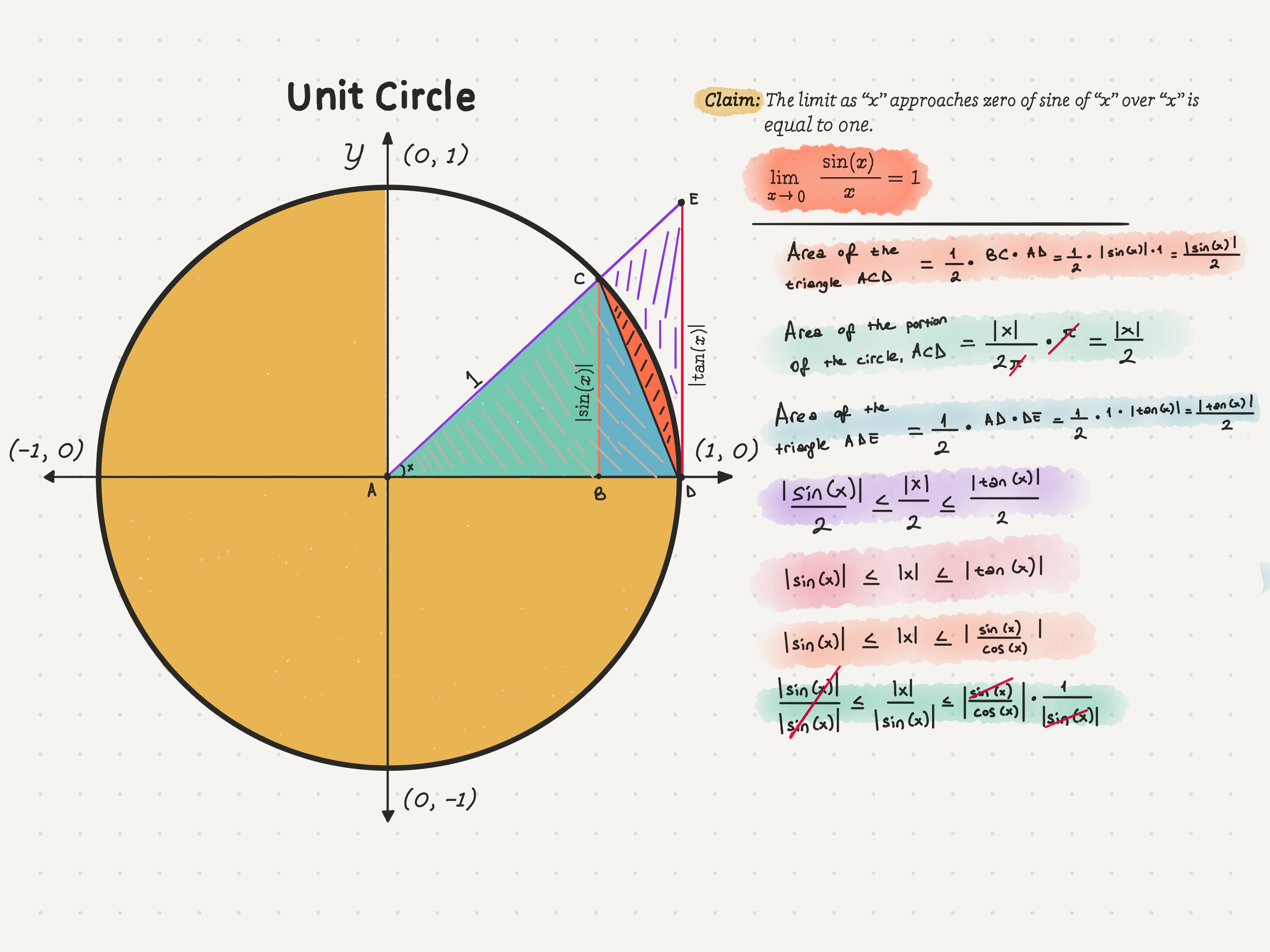
Note: Since we’re dividing by a positive quantity, it’s not going to change the direction of the inequalities.
We can now achieve 1 ≤ x/|sin(x)| ≤ 1/|cos(x)| by simplifying our latest inequality.
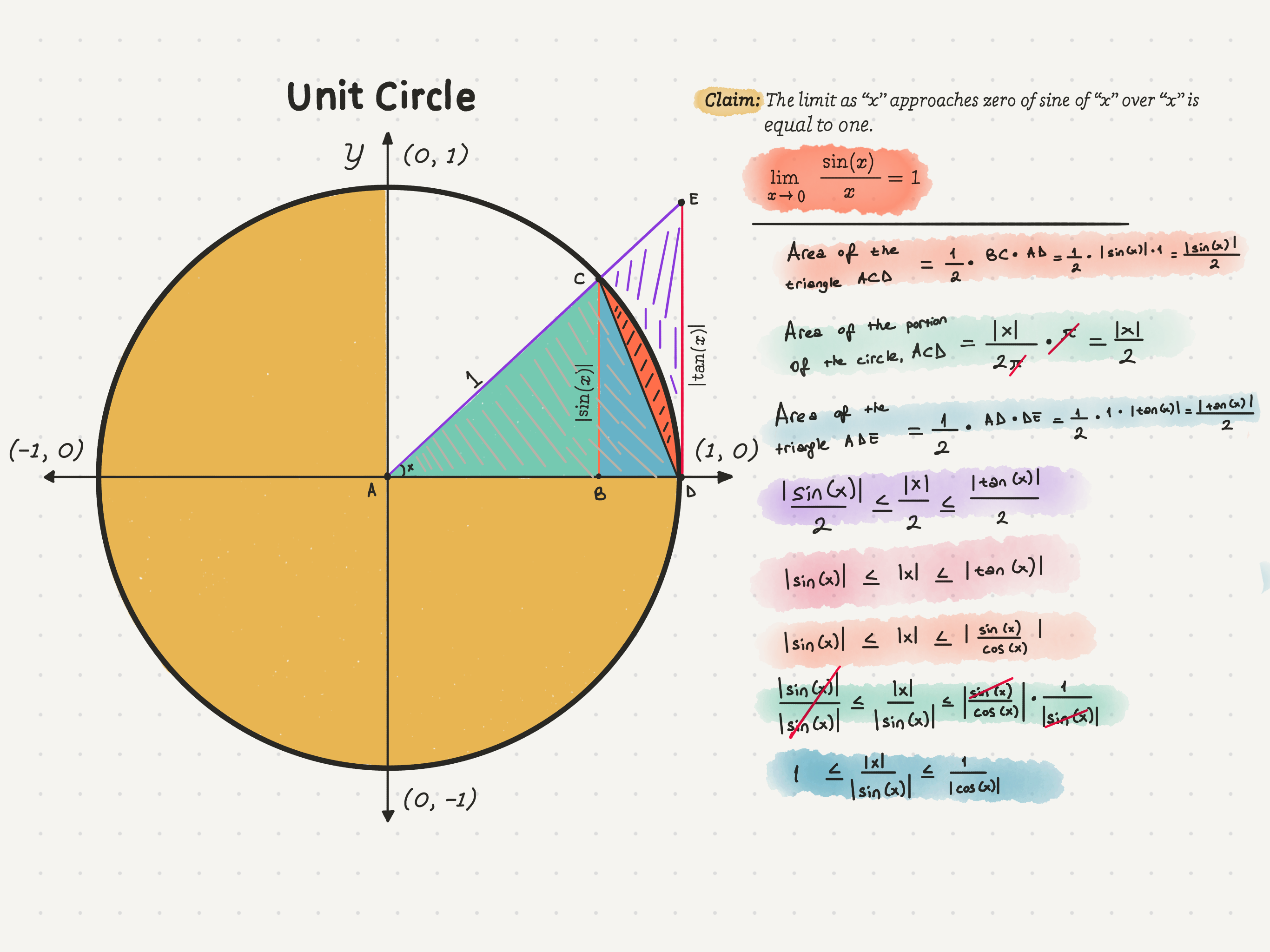
At this point, it is essential to remember our purpose. Remember, we want to prove the “sin of x over x.” If you look at the inequality, we realize that we have “x over the sin of x.” In this situation, there is one thing you have to remember. Yes, reciprocals.
Reciprocal: The multiplicative inverse. If you take the reciprocal of a fraction a/b, you get b/a.If we take the reciprocal of everything, we get the “sin of x over x.” There is one thing we mustn’t forget, though, changing the direction of the inequality. Thus, the less than or equal to sign will turn into the greater than or equal to sign.
We are lucky because the reciprocal of 1 is still 1. Therefore, the new inequality is as follows.
1 ≥ |sin(x)|/x ≥ |cos(x)|
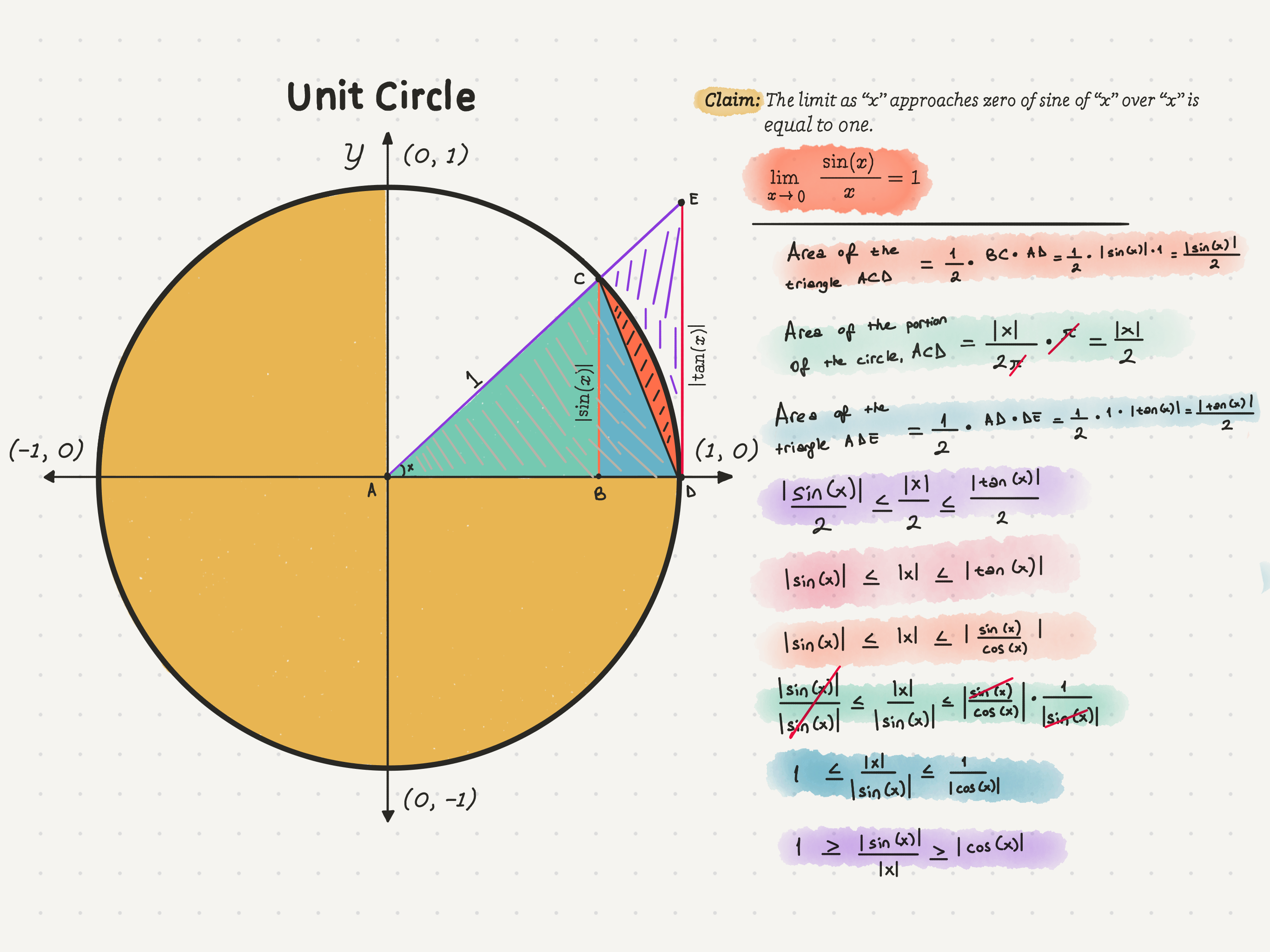
Note: We only care about the first and fourth quadrants. In the first quadrant, the sin of “x” and “x” are both positive. In the fourth quadrant, they’re both negative, but you’re going to get a positive value when you divide them. So we can erase those absolute value signs. Also, since the cosine value is also positive, we can get rid of the absolute value signs.
1 ≥ sin(x)/x ≥ cos(x)Hang on, hang on. We are almost done. In the inequality, all of the terms represent functions.
Therefore, we can say that f(x) = 1, g(x) = sin(x)/x, and h(x) = cos(x). We say this because if we want to find the limits we have been looking for, we need to rely on some theorems.
Meaning that if in one inequality, the limits of both the left and the right functions are approaching the same value, the middle function’s limit also has to approach to thesame value.1 ≥ sin(x)/x ≥ cos(x)
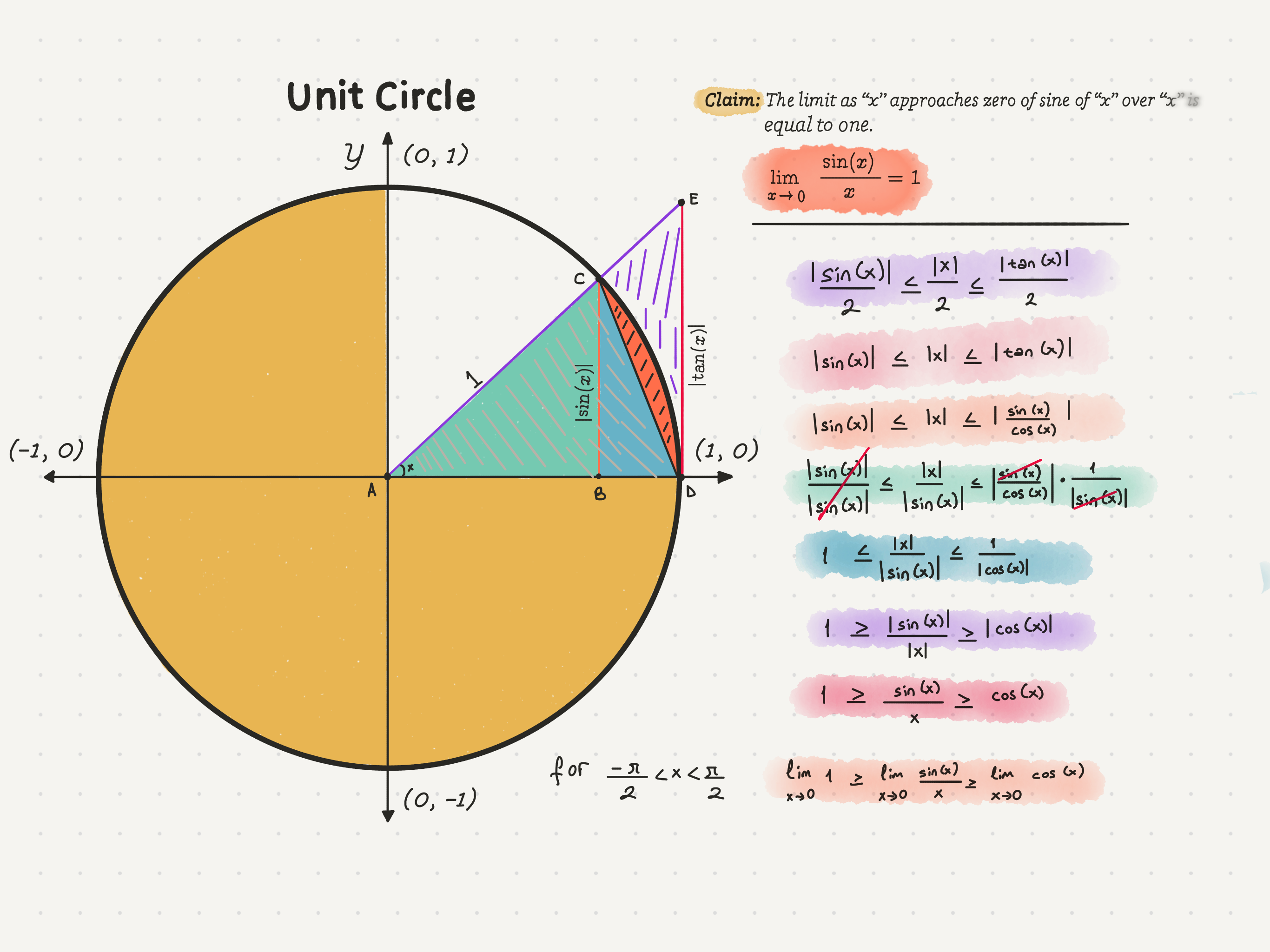
Therefore, if we look at our inequality, it is clear that the first function, f(x), approaches 1. How about h(x)? Meaning, what is the limit as x approaches zero of cosine x? Yes, the cosine of zero is just one, and cosine is a continuous function. Therefore, the limit is 1.
So our limit is going to be less than or equal to one. It is also going to be greater than or equal to one. Therefore, it must be equal to one.

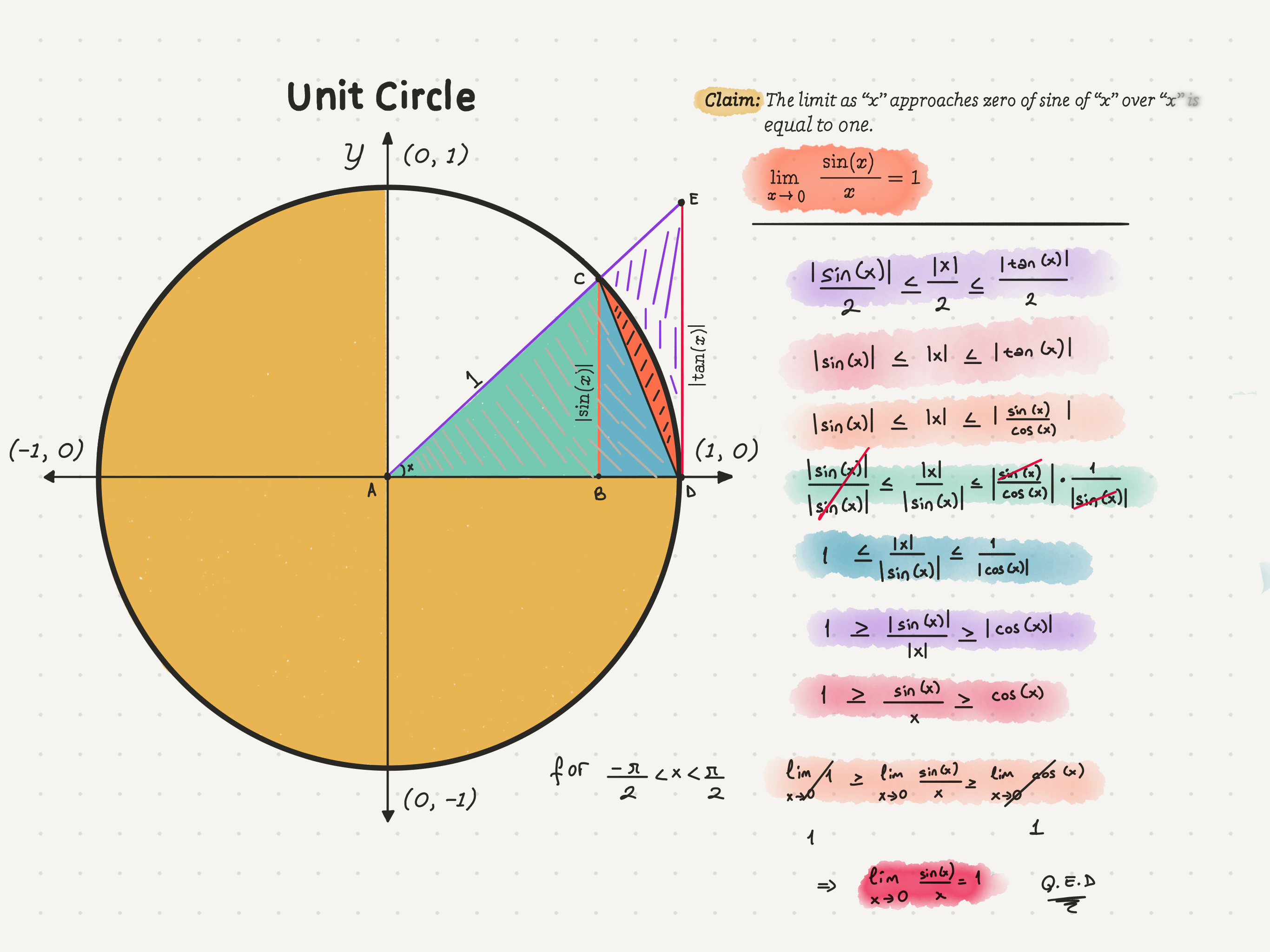
We are now done!

![{\displaystyle \pi ={\frac {9801}{2{\sqrt {2}}\displaystyle \sum _{n=0}^{\infty }{\frac {(4n)!}{(n!)^{4}}}\times {\frac {[1103+26390n]}{(4\times 99)^{4n}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ff69018803625bc5b3d88da7f0e0c02ce732959)



